
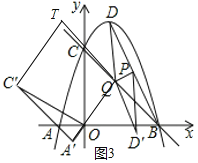
【题目】如图1,已知抛物线![]() 与x轴交于A、B两点,与y轴交于点C,顶点为D,连接BC
与x轴交于A、B两点,与y轴交于点C,顶点为D,连接BC
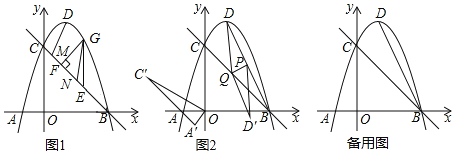
![]() 点G是直线BC上方抛物线上一动点
点G是直线BC上方抛物线上一动点![]() 不与B、C重合
不与B、C重合![]() ,过点G作y轴的平行线交直线BC于点E,作
,过点G作y轴的平行线交直线BC于点E,作![]() 于点F,点M、N是线段BC上两个动点,且
于点F,点M、N是线段BC上两个动点,且![]() ,连接DM、
,连接DM、![]() 当
当![]() 的周长最大时,求
的周长最大时,求![]() 的最小值;
的最小值;
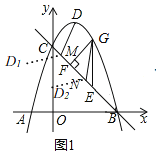
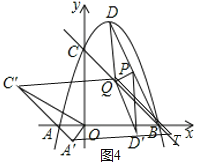
![]() 如图2,连接BD,点P是线段BD的中点,点Q是线段BC上一动点,连接DQ,将
如图2,连接BD,点P是线段BD的中点,点Q是线段BC上一动点,连接DQ,将![]() 沿PQ翻折,且线段
沿PQ翻折,且线段![]() 的中点恰好落在线段BQ上,将
的中点恰好落在线段BQ上,将![]() 绕点O逆时针旋转
绕点O逆时针旋转![]() 得到
得到![]() ,点T为坐标平面内一点,当以点Q、
,点T为坐标平面内一点,当以点Q、![]() 、
、![]() 、T为顶点的四边形是平行四边形时,求点T的坐标.
、T为顶点的四边形是平行四边形时,求点T的坐标.
【答案】(1)![]() 最小值为
最小值为![]() ;(2)点T的坐标为
;(2)点T的坐标为![]() 或
或![]() 或
或![]()
【解析】
![]() 先求出点B、C、D的坐标,可求直线BC解析式且得到
先求出点B、C、D的坐标,可求直线BC解析式且得到![]() 由
由![]() 轴和
轴和![]() 可得
可得![]() 是等腰直角三角形,则GE最大时其周长最大
是等腰直角三角形,则GE最大时其周长最大![]() 设点G坐标为
设点G坐标为![]() ,则点
,则点![]() ,可列得GE与a的函数关系式,配方可求出其最大值,得到此时的G坐标和EF的长,即得到MN长
,可列得GE与a的函数关系式,配方可求出其最大值,得到此时的G坐标和EF的长,即得到MN长![]() 求
求![]() 最小值转化为求
最小值转化为求![]() 最小值
最小值![]() 先作D关于直线BC的对称点
先作D关于直线BC的对称点![]() ,再通过平移
,再通过平移![]() 得
得![]() ,构造“将军饮马”的基本图形求解.
,构造“将军饮马”的基本图形求解.
![]() 由翻折得DD′⊥PQ,PD=PD′,再由P为BD中点证得∠BD′D=90°,得PQ//BD′,又D′P中点H在BQ上,可证
由翻折得DD′⊥PQ,PD=PD′,再由P为BD中点证得∠BD′D=90°,得PQ//BD′,又D′P中点H在BQ上,可证![]() ≌△D′BH,所以有D′Q//BP,即四边形DQ D′P为菱形,得
≌△D′BH,所以有D′Q//BP,即四边形DQ D′P为菱形,得![]() 设Q点坐标为
设Q点坐标为![]() 即可列方程求得
即可列方程求得![]() 再根据题意把点A′、C′求出
再根据题意把点A′、C′求出![]() 以点Q、
以点Q、![]() 、
、![]() 、T为顶点的四边形是平行四边形,要进行分类讨论,结合图形,利用平行四边形对边平行的性质,用平移坐标的方法即可求得点T.
、T为顶点的四边形是平行四边形,要进行分类讨论,结合图形,利用平行四边形对边平行的性质,用平移坐标的方法即可求得点T.
![]() ,
,
![]() 抛物线与x轴交于点
抛物线与x轴交于点![]() 、点
、点![]() ,与y轴交于点
,与y轴交于点![]() ,顶点
,顶点![]() ,
,
![]() 直线CB解析式:
直线CB解析式:![]() ,
,![]() ,
,
![]() 轴,
轴,![]() ,
,
![]() ,
,![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
![]() ,
,
设点![]() ,则点
,则点![]() ,其中
,其中![]() ,
,
![]() ,
,
![]() 时,GE有最大值为
时,GE有最大值为![]() ,
,
![]() 的周长最大时,
的周长最大时,![]() ,
,![]() ,
,
![]() ,E点可看作点F向右平移
,E点可看作点F向右平移![]() 个单位、向下平移
个单位、向下平移![]() 个单位,
个单位,
如图1,作点D关于直线BC的对称点![]() ,过N作
,过N作![]() 且
且![]() ,
,
![]() ,
,![]() 即
即![]()
![]() ,
,
![]() 当
当![]() 、N、G在同一直线上时,
、N、G在同一直线上时,![]() 为最小值,
为最小值,
![]() ,
,
![]() 最小值为
最小值为![]() ;
;
![]() 连接DD′、D′B,设D′P与BQ交点为
连接DD′、D′B,设D′P与BQ交点为![]() 如图
如图![]() ,
,
![]() 沿PQ翻折得△D′PQ,
沿PQ翻折得△D′PQ,
∴DD′⊥PQ,PD=PD′,DQ=D′Q,∠DQP=∠D′QP,
![]() 为BD中点,
为BD中点,
∴PB=PD=PD′,![]() ,
,
∴△BDD′是直角三角形,∠BD′D=90°,
∴PQ//BD′,
∴∠PQH=∠D′BH,
![]() 为D′P中点,
为D′P中点,
∴PH=D′H,
在![]() 与△D′BH中
与△D′BH中
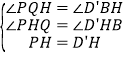 ,
,
![]() ≌△D′BH (AAS),
≌△D′BH (AAS),
∴PQ=BD′,
![]() 四边形BPQD′是平行四边形,
四边形BPQD′是平行四边形,
∴D′Q//BP,
∴∠DPQ=∠D′QP,
![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,
解得:![]() ,
,![]() 舍去
舍去![]() ,
,
![]() 点Q坐标为
点Q坐标为![]() ,
,
![]() 绕点O逆时针旋转
绕点O逆时针旋转![]() 得到
得到![]() ,
,
∴A′![]() ,C′
,C′![]() ,
,
∴A′、C′横坐标差为![]() ,纵坐标差为
,纵坐标差为![]() ,
,
A′、Q横坐标差为![]() ,纵坐标差为
,纵坐标差为![]() ,
,
当有平行四边形A′C′TQ时![]() 如图
如图![]() ,点T横坐标为
,点T横坐标为![]() ,纵坐标为
,纵坐标为![]() ;
;
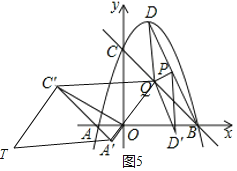
当有平行四边形A′C′QT时![]() 如图
如图![]() ,点T横坐标为
,点T横坐标为![]() ,纵坐标为
,纵坐标为![]() ;
;
当有平行四边形A′TC′Q时![]() 如图
如图![]() ,点T横坐标为
,点T横坐标为![]() ,纵坐标为
,纵坐标为![]() ,
,
综上所述,点T的坐标为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
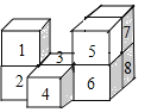
【题目】如图,是用8个大小相同的小正方体搭成的几何体,仅在该几何体中取走一块小正方体,使得到的新几何体同时满足两个要求:(1)从正面看到的形状和原几何体从正面看到的形状相同;(2)从左面看到的形状和原几何体从左面看到的形状也相同.在不改变其它小正方体位置的前提下,可取走的小正方体的标号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
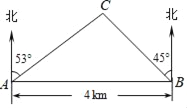
【题目】如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东53°方向上,从B测得灯塔C在北偏西45°方向上,求灯塔C与观测点A的距离(精确到0.1km).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题:
(1)请按要求对△ABO作如下变换:
①将△OAB向下平移2个单位,再向左平移3个单位得到△O1A1B1;
②以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△OA2B2.
(2)写出点A1,A2的坐标: , ;
(3)△OA2B2的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料,回答问题:
材料一:我们将![]() 与
与![]() 称为一对“对偶式”因为
称为一对“对偶式”因为![]() ,所以构造“对俩式”相乘可以有效地将
,所以构造“对俩式”相乘可以有效地将![]() 和
和![]() 中的
中的![]() 去掉.例如:已知
去掉.例如:已知![]() ,求
,求![]()
![]() 的值.解:
的值.解:![]() ,
,![]()
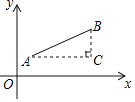
材料二:如图,点![]() ,点
,点![]() ,以AB为斜边作
,以AB为斜边作![]() ,则
,则![]() ,于是
,于是![]() ,
,![]() ,所以
,所以![]() .反之,可将代数式
.反之,可将代数式![]() 的值看作点
的值看作点![]() 到点
到点![]() 的距离.
的距离.
例如:![]() =
=![]() .
.
所以可将代数式![]() 的值看作点
的值看作点![]() 到点
到点![]() 的距离.
的距离.
![]() 利用材料一,解关于x的方程:
利用材料一,解关于x的方程:![]() ,其中
,其中![]() ;
;
![]() 利用材料二,求代数式
利用材料二,求代数式![]() 的最小值,并求出此时y与x的函数关系式,写出x的取值范图;
的最小值,并求出此时y与x的函数关系式,写出x的取值范图;
![]() 将
将![]() 所得的y与x的函数关系式和x的取值范围代入
所得的y与x的函数关系式和x的取值范围代入![]() 中解出x,直接写出x的值.
中解出x,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.
(1)抛物线的对称轴与x轴的交点E坐标为_____,点A的坐标为_____;
(2)若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;
(3)在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“铁路建设助推经济发展”,近年来我国政府十分重视铁路建设.渝利铁路通车后,从重庆到上海比原铁路全程缩短了320千米,列车设计运行时速比原铁路设计运行时速提高了120千米/小时,全程设计运行时间只需8小时,比原铁路设计运行时间少用16小时.
(1)渝利铁路通车后,重庆到上海的列车设计运行里程是多少千米?
(2)专家建议:从安全的角度考虑,实际运行时速减少m%,以便于有充分时间应对突发事件,这样,从重庆到上海的实际运行时间将增加![]() m%小时,求m的值.
m%小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
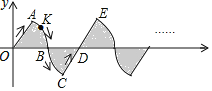
【题目】在平面直角坐标系xOy中,若干个半径为1个单位长度,圆心角是![]() 的扇形按图中的方式摆放,动点K从原点O出发,沿着“半径OA
的扇形按图中的方式摆放,动点K从原点O出发,沿着“半径OA![]() 弧AB
弧AB![]() 弧BC
弧BC![]() 半径CD
半径CD![]() 半径DE
半径DE![]() ”的曲线运动,若点K在线段上运动的速度为每秒1个单位长度,在弧线上运动的速度为每秒
”的曲线运动,若点K在线段上运动的速度为每秒1个单位长度,在弧线上运动的速度为每秒![]() 个单位长度,设第n秒运动到点K,
个单位长度,设第n秒运动到点K,![]() 为自然数
为自然数![]() ,则
,则![]() 的坐标是____,
的坐标是____,![]() 的坐标是____
的坐标是____
查看答案和解析>>
科目:初中数学 来源: 题型:
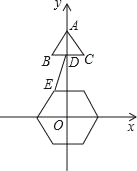
【题目】如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )
A. 3 B. 4﹣![]() C. 4 D. 6﹣2
C. 4 D. 6﹣2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com