
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣ ![]() x+
x+ ![]() 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 .
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 . 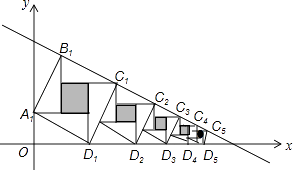
【答案】![]()
【解析】解:设第n个大正方形的边长为an , 则第n个阴影小正方形的边长为 ![]() an , 当x=0时,y=﹣
an , 当x=0时,y=﹣ ![]() x+
x+ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() a1+
a1+ ![]() a1 ,
a1 ,
∴a1= ![]() .
.
∵a1=a2+ ![]() a2 ,
a2 ,
∴a2= ![]()
![]() ,
,
同理可得:a3= ![]() a2 , a4=
a2 , a4= ![]() a3 , a5=
a3 , a5= ![]() a4 , …,
a4 , …,
∴an= ![]() a1=
a1= ![]()
![]() ,
,
∴第n个阴影小正方形的面积为 ![]() =
= ![]() =
= ![]() .
.
故答案为: ![]() .
.
设第n个大正方形的边长为an , 则第n个阴影小正方形的边长为 ![]() an , 根据一次函数图象上点的坐标特征即可求出直线y=﹣
an , 根据一次函数图象上点的坐标特征即可求出直线y=﹣ ![]() x+
x+ ![]() 与y轴的交点坐标,进而即可求出a1的值,再根据相似三角形的性质即可得出an=
与y轴的交点坐标,进而即可求出a1的值,再根据相似三角形的性质即可得出an= ![]() a1=
a1= ![]()
![]() ,结合正方形的面积公式即可得出结论.
,结合正方形的面积公式即可得出结论.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)画出将△OAB绕原点旋转180°后所得的△OA1B1 , 并写出点B1的坐标;
(2)将△OAB平移得到△O2A2B2 , 点A的对应点是A2(2,﹣4),点B的对应点B2在坐标系中画出△O2A2B2;并写出B2的坐标;
(3)△OA1B1与△O2A2B2成中心对称吗?若是,请直接写出对称中心点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2 , 以直线l1上的点A为圆心、适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC.若∠ABC=67°,则∠1=( ) 
A.23°
B.46°
C.67°
D.78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批秋衣,价格为每件30元.物价部门规定其销售单价不高于每件60元,不低于每件30元.经市场调查发现:日销售量y(件)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)求该服装店销售这批秋衣日获利w(元)与销售单价x(元)之间的函数关系式.
(3)当销售单价为多少元时,该服装店日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A,且点A的横坐标为4.
的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A,且点A的横坐标为4. 
(1)求点A的坐标及一次函数的解析式;
(2)若直线x=2与反比例函数和一次函数的图象分别交于点B、C,求线段BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com