
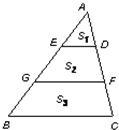
 5、如图,DE∥FG∥BC,AE=EG=BG,则S1:S2:S3=( )
5、如图,DE∥FG∥BC,AE=EG=BG,则S1:S2:S3=( )

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源:2013-2014学年山东青岛超银中学(广饶路校区)九年级第一学期月考数学试卷(解析版) 题型:填空题
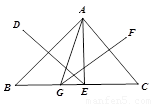
如图,DE,FG分别是△ABC的AB,AC边的垂直平分线,连接AG,AE,已知BC=10,GE=2,∠BAC=80°,则∠GAE= ,△AGE的周长是
查看答案和解析>>
科目:初中数学 来源:2012年沪科版初中数学九年级上24.3相似三角形的性质练习卷(解析版) 题型:选择题
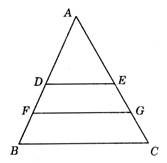
如图,DE∥FG∥BC,且DE、FG把△ABC的面积三等分,若BC=12,则FG的长是( ).
A.8 B.6 C.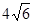 D.
D.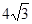
查看答案和解析>>
科目:初中数学 来源:2003年广东省广州市中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com