
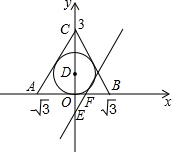 在平面直角坐标系中,△ABC三个顶点坐标为A(-$\sqrt{3}$,0)、B($\sqrt{3}$,0)、C(0,3).
在平面直角坐标系中,△ABC三个顶点坐标为A(-$\sqrt{3}$,0)、B($\sqrt{3}$,0)、C(0,3).分析 (1)由A、B、C三点坐标可知∠CBO=60°,又因为点D是△ABC的内心,所以BD平分∠CBO,然后利用锐角三角函数即可求出OD的长度;
(2)根据题意可知,DF为半径,且∠DFE=90°,过点F作FG⊥y轴于点G,求得FG和OG的长度,即可求出点F的坐标,然后将E和F的坐标代入一次函数解析式中,即可求出直线EF的解析式;
(3)⊙P上存在一点到△ABC三个顶点的距离相等,该点是△ABC的外接圆圆心,即为点D,所以DP=2$\sqrt{7}$,又因为点P在直线EF上,所以这样的点P共有2个,且由勾股定理可知PF=3$\sqrt{3}$.
解答 解: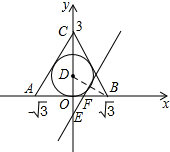 (1)连接BD,
(1)连接BD,
∵B($\sqrt{3}$,0),C(0,3),
∴OB=$\sqrt{3}$,OC=3,
∴tan∠CBO=$\frac{OC}{OB}$=$\sqrt{3}$,
∴∠CBO=60°
∵点D是△ABC的内心,
∴BD平分∠CBO,
∴∠DBO=30°,
∴tan∠DBO=$\frac{OD}{OB}$,
∴OD=1,
∴△ABC内切圆⊙D的半径为1;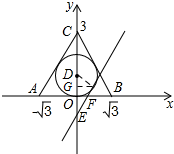 (2)连接DF,
(2)连接DF,
过点F作FG⊥y轴于点G,
∵E(0,-1)
∴OE=1,DE=2,
∵直线EF与⊙D相切,
∴∠DFE=90°,DF=1,
∴sin∠DEF=$\frac{DF}{DE}$,
∴∠DEF=30°,
∴∠GDF=60°,
∴在Rt△DGF中,
∠DFG=30°,
∴DG=$\frac{1}{2}$,
由勾股定理可求得:GF=$\frac{\sqrt{3}}{2}$,
∴F($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
设直线EF的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{b=-1}\\{\frac{1}{2}=\frac{\sqrt{3}}{2}k+b}\end{array}\right.$,
∴直线EF的解析式为:y=$\sqrt{3}$x-1;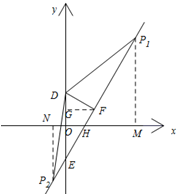 (3)∵⊙P上存在一点到△ABC三个顶点的距离相等,
(3)∵⊙P上存在一点到△ABC三个顶点的距离相等,
∴该点必为△ABC外接圆的圆心,
由(1)可知:△ABC是等边三角形,
∴△ABC外接圆的圆心为点D
∴DP=2$\sqrt{7}$,
设直线EF与x轴交于点H,
∴令y=0代入y=$\sqrt{3}$x-1,
∴x=$\frac{\sqrt{3}}{3}$,
∴H($\frac{\sqrt{3}}{3}$,0),
∴FH=$\frac{\sqrt{3}}{3}$,
当P在x轴上方时,
过点P1作P1M⊥x轴于M,
由勾股定理可求得:P1F=3$\sqrt{3}$,
∴P1H=P1F+FH=$\frac{10\sqrt{3}}{3}$,
∵∠DEF=∠HP1M=30°,
∴HM=$\frac{1}{2}$P1H=$\frac{5\sqrt{3}}{3}$,P1M=5,
∴OM=2$\sqrt{3}$,
∴P1(2$\sqrt{3}$,5),
当P在x轴下方时,
过点P2作P2N⊥x轴于点N,
由勾股定理可求得:P2F=3$\sqrt{3}$,
∴P2H=P2F-FH=$\frac{8\sqrt{3}}{3}$,
∴∠DEF=30°
∴∠OHE=60°
∴sin∠OHE=$\frac{{P}_{2}N}{{P}_{2}H}$,
∴P2N=4,
令y=-4代入y=$\sqrt{3}$x-1,
∴x=-$\sqrt{3}$,
∴P2(-$\sqrt{3}$,-4),
综上所述,若⊙P上存在一点到△ABC三个顶点的距离相等,此时圆心P的坐标为(2$\sqrt{3}$,5)或(-$\sqrt{3}$,-4).
点评 本题是圆的综合问题,涉及圆的外接圆和内切圆的相关性质,圆的切线性质,锐角三角函数,一次函数等知识,综合程度较高,需要学生将各知识点灵活运用.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
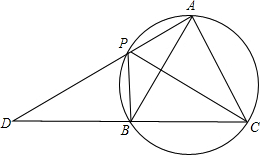 如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | x | C. | $\frac{1}{x}$ | D. | $\frac{x+2}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
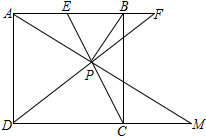 如图,点P为正方形ABCD内一点,且∠APB=90°,延长AP交直线CD于M,分别延长CP、DP交直线AB于点E、F
如图,点P为正方形ABCD内一点,且∠APB=90°,延长AP交直线CD于M,分别延长CP、DP交直线AB于点E、F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com