
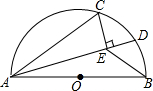
 如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是$\widehat{BC}$上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为$\sqrt{13}$-2.
如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是$\widehat{BC}$上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为$\sqrt{13}$-2. 分析 如图,连接BO′、BC.在点D移动的过程中,点E在以AC为直径的圆上运动,当O′、E、B共线时,BE的值最小,最小值为O′B-O′E,利用勾股定理求出BO′即可解决问题.
解答 解:如图,连接BO′、BC.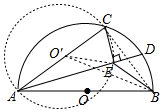
∵CE⊥AD,
∴∠AEC=90°,
∴在点D移动的过程中,点E在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AC=4,AB=5,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
在Rt△BCO′中,BO′=$\sqrt{B{C}^{2}+CO{′}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∵O′E+BE≥O′B,
∴当O′、E、B共线时,BE的值最小,最小值为O′B-O′E=$\sqrt{13}$-2,
故答案为:$\sqrt{13}-2$.
点评 本题考查圆综合题、勾股定理、点与圆的位置关系等知识,解题的关键是确定等E的运动轨迹是以AC为直径的圆上运动,属于中考填空题中 压轴题.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:选择题
| A. | 1440毫升 | B. | 1.4×103毫升 | C. | 0.14×104毫升 | D. | 14×102毫升 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=1,n=0 | B. | m=3,n=-4 | C. | m=1,n=-2 | D. | m=3,n=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
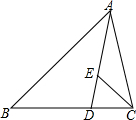 在△ABC中,∠B=45°,点D在边BC上,AD=AC,点E在边AD上,∠BCE=45°,若AB=5$\sqrt{2}$.AE=2DE,则AC=$\sqrt{26}$.
在△ABC中,∠B=45°,点D在边BC上,AD=AC,点E在边AD上,∠BCE=45°,若AB=5$\sqrt{2}$.AE=2DE,则AC=$\sqrt{26}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 探测船上的声呐发出的超声波以1450m/s的速度射向海底,海底再将超声波反射回来,经ts后声呐收到反射超声波.试求海底深度hm与时间ts之间的关系.
探测船上的声呐发出的超声波以1450m/s的速度射向海底,海底再将超声波反射回来,经ts后声呐收到反射超声波.试求海底深度hm与时间ts之间的关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com