
【题目】如图已知△CAB和△CDE中,CA=CB,CD=CE,∠BCA=∠DCE=![]() .连BE,BD.
.连BE,BD.
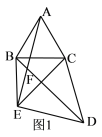
(1)如图1,若∠BCA=60![]() ,BD与AE交于点F,求∠AFB的度数;
,BD与AE交于点F,求∠AFB的度数;
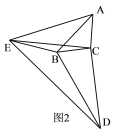
(2)如图2,请探究∠EBD,∠AEB与![]() 之间的关系;
之间的关系;
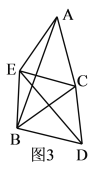
(3)如图3,直接写出∠EBD,∠AEB与![]() 之间的关系.
之间的关系.
【答案】(1)60![]() ;(2)∠EBD-∠AEB=
;(2)∠EBD-∠AEB=![]() ;(3)∠EBD+∠AEB+
;(3)∠EBD+∠AEB+![]() =360
=360![]() .
.
【解析】
(1)∠ACE=∠ACB+∠BCE=∠DCE+∠BCE=∠BCD,再由AC=BC和CE=CD可证明△ACE≌BCD,则∠CAE=∠CBD,由图可知∠CAE+∠ACB=∠CBD+∠BFA,则∠AFB=∠ACB=60°;
(2)由AC=BC,EC=DC且∠ACE=∠α-∠ECB=∠BCD,易证△ACE≌BCD,则∠AEC=∠BDC,再由∠EBD=∠CEB+∠CDB+∠ECD可得
∠EBD=∠AEB+∠ECD=∠AEB+![]() ,则∠EBD-∠AEB=
,则∠EBD-∠AEB=![]() ;
;
(3)同上易证△ACE≌BCD,从而∠CAE=∠CBD,由四边形ECDB的内角和定理可得∠CEB+∠CBD+∠ECD+∠BDC=360°,则∠EBD+∠AEB+![]() =360
=360![]() .
.
(1)∵∠ACE=∠ACB+∠BCE,∠BCD=∠DCE+∠BCE,
∴∠ACE=∠BCD,
又∵AC=BC,CE=CD,
∴△ACE≌BCD,
∴∠CAE=∠CBD,
∵∠CAE+∠ACB=∠CBD+∠BFA,
∴∠AFB=∠ACB=60°.
(2)∠EBD-∠AEB=![]() .
.
证明:
∵∠ACE=∠ACB-∠BCE,∠BCD=∠DCE-∠BCE,
∴∠ACE=∠BCD,
又∵AC=BC,CE=CD,
∴△ACE≌BCD,
∴∠AEC=∠BDC,
∵∠EBD=∠CEB+∠CDB+∠ECD,
∴∠EBD=∠AEB+∠ECD=∠AEB+![]() ,
,
即∠EBD-∠AEB=![]() .
.
(3)∠EBD+∠AEB+![]() =360
=360![]() .
.
∵∠ACE=∠ACB-∠BCE,∠BCD=∠DCE-∠BCE,
∴∠ACE=∠BCD,
又∵AC=BC,CE=CD,
∴△ACE≌BCD,
∴∠CAE=∠CBD,
在四边形ECDB中,
∵∠CEB+∠CBD+∠ECD+∠BDC=360°,
∴∠EBD+∠AEB+![]() =360
=360![]() .
.


科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好. 
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF. 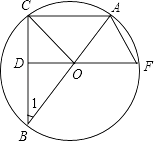
(1)求证:△COD≌△BOD;
(2)填空:①当∠1=时,四边形OCAF是菱形; ②当∠1=时,AB=2 ![]() OD.
OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,一组互相平行的直线共有n条(n≥2,且n为正整数),它们和两条平行线a,b相交,构成若干个“#”字形. 设构成的“#”字形的个数为x,请找出规律,并填写下表.

n | 2 | 3 | 4 | 5 | … | n |
x | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读理解】
我们知道,当a>0且b>0时,( ![]() ﹣
﹣ ![]() )2≥0,所以a﹣2
)2≥0,所以a﹣2 ![]() +≥0,从而a+b≥2
+≥0,从而a+b≥2 ![]() (当a=b时取等号),
(当a=b时取等号),
【获得结论】设函数y=x+ ![]() (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x= ![]() 即x=
即x= ![]() 时,函数y有最小值为2
时,函数y有最小值为2 ![]()
(1)【直接应用】
若y1=x(x>0)与y2= ![]() (x>0),则当x=时,y1+y2取得最小值为 .
(x>0),则当x=时,y1+y2取得最小值为 .
(2)【变形应用】
若y1=x+1(x>﹣1)与y2=(x+1)2+4(x>﹣1),则 ![]() 的最小值是
的最小值是
(3)【探索应用】
在平面直角坐标系中,点A(﹣3,0),点B(0,﹣2),点P是函数y= ![]() 在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S
在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S
①求S与x之间的函数关系式;
②求S的最小值,判断取得最小值时的四边形ABCD的形状,并说明理由.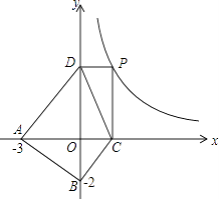
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,按学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题: 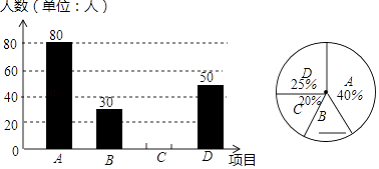
(1)本次共调查了名学生;
(2)在扇形统计图中,“B”所在扇形的圆心角是度;
(3)将条形统计图补充完整;
(4)若该中学有1200名学生,喜欢篮球运动的学生约有名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com