试题分析:解:根据每行的第一个数分别为:2,4=2
2,8=2
3,……所以第m行头个数为2
m第1行
| 2
|
第2行
| 4 6
|
第3行
| 8 10 12 14
|
第4行
| 16,18,20,22,24,26,28,30,
|
第5行
| 32,34,36,38,40,42,44,……62.
|
第m行后面第n个数字比上一行第n个数字多2
m-1则(4,3)所表示的数是:第4行第3个数为:因为第3行第3个数是12,所以2
3=8,故第3个数为:12+2
4-1=20;
(5,6)所表示的数是:∵第4行第6个数为26,且2
4=32,∴第6个数为:26+16=42;
(6,5)所表示的数是:∵第5行第5个数为:40,且2
6-1=32∴第5个数为40+2
6-1=72;
∴(5,6)与(6,5)表示的两数之积是:42×72=3024;
则可知数字P=2
m+2n且每m行的数字个数为:1=2
0,2=2
1,4=2
2,…第n行为:2
n-1,
前十行首个数字为2,4,8,16,32,64,128,256,512,1024.
第十行第二个数字:512+512+2=1026,所以第三个数字为1028.
则第10行3个数为1028.
点评:本题难度较大,属于能力提升题,此类题目有利于培养学生的综合能力。解题的关键在于分析数字,以及相应数字之间的关系。

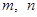 )表示第
)表示第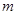 行从左向右第
行从左向右第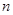 个数,则(4,3)所表示的数是_________;(5,6)与(6,5)表示的两数之积是_________,数1028对应的坐标号是_________ .
个数,则(4,3)所表示的数是_________;(5,6)与(6,5)表示的两数之积是_________,数1028对应的坐标号是_________ .

 阅读快车系列答案
阅读快车系列答案