
科目:初中数学 来源: 题型:填空题
 如图,完全一样的矩形的顶点都落在平面直角坐标系中方格的格点处,按照如图所示的方式标注字母.
如图,完全一样的矩形的顶点都落在平面直角坐标系中方格的格点处,按照如图所示的方式标注字母.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 对于正实数a,b;($\frac{a+b}{2}$)2-ab=$\frac{{a}^{2}+2ab+{b}^{2}}{4}$-$\frac{4ab}{4}$=$\frac{{a}^{2}-2ab+{b}^{2}}{4}$=($\frac{a-b}{2}$)2
对于正实数a,b;($\frac{a+b}{2}$)2-ab=$\frac{{a}^{2}+2ab+{b}^{2}}{4}$-$\frac{4ab}{4}$=$\frac{{a}^{2}-2ab+{b}^{2}}{4}$=($\frac{a-b}{2}$)2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,-6) | B. | (-6,3) | C. | (6,3) | D. | (-6,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
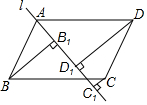 如图,过?ABCD的顶点A作直线l.
如图,过?ABCD的顶点A作直线l.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
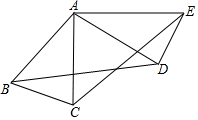 如图,△ABC中,AB=AC,∠ABC=70°.△ABC绕点A按逆时针方向旋转一定角度后,得到△ADE.问:
如图,△ABC中,AB=AC,∠ABC=70°.△ABC绕点A按逆时针方向旋转一定角度后,得到△ADE.问:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将正方形ABCG和正方形CDEF按图中虚线剪拼成一个正方形AHEP,若这个新正方形AHEP的面积为13,正方形CDEF的边长为2,则正方形ABCG的边长为( )
如图,将正方形ABCG和正方形CDEF按图中虚线剪拼成一个正方形AHEP,若这个新正方形AHEP的面积为13,正方形CDEF的边长为2,则正方形ABCG的边长为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | $\sqrt{11}$ | D. | $\sqrt{15}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com