
【题目】传统的端午节即将来临,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足如下关系:
y=![]()
(1)李明第几天生产的粽子数量为280只?
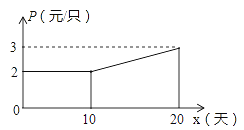
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
【答案】(1)李明第10天生产的粽子数量为280只.(2)第13天的利润最大,最大利润是578元.
【解析】(1)把y=280代入y=20x+80,解方程即可求得;
(2)根据图象求得成本p与x之间的关系,然后根据利润等于订购价减去成本价,然后整理即可得到W与x的关系式,再根据一次函数的增减性和二次函数的增减性解答.
(1)设李明第x天生产的粽子数量为280只,
由题意可知:20x+80=280,
解得x=10.
答:第10天生产的粽子数量为420只.
(2)由图象得,当0≤x<10时,p=2;
当10≤x≤20时,设P=kx+b,
把点(10,2),(20,3)代入得,
![]() ,
,
解得![]() ,
,
∴p=0.1x+1,
①0≤x≤6时,w=(4-2)×34x=68x,当x=6时,w最大=408(元);
②6<x≤10时,w=(4-2)×(20x+80)=40x+160,
∵x是整数,
∴当x=10时,w最大=560(元);
③10<x≤20时,w=(4-0.1x-1)×(20x+80)=-2x2+52x+240,
∵a=-3<0,
∴当x=-![]() =13时,w最大=578(元);
=13时,w最大=578(元);
综上,当x=13时,w有最大值,最大值为578.


科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,有下列结论:①
的图象如图所示,有下列结论:①![]() ;②
;②![]() ;③若
;③若![]() 为任意实数,则
为任意实数,则![]() ;④a-b+c>0;⑤若
;④a-b+c>0;⑤若![]() ,且
,且![]() ,则
,则![]() .其中,正确结论的个数为( )
.其中,正确结论的个数为( )
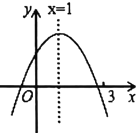
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() 三点.点
三点.点![]() 是抛物线
是抛物线![]() 段上一动点(不含端点
段上一动点(不含端点![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]()
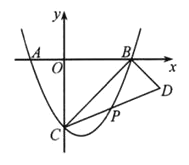
(1)求抛物线的解析式.
(2)当![]() 时,求点
时,求点![]() 的坐标。
的坐标。
(3)在(2)的条件下,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017山东日照)已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )

A. ①②③ B. ③④⑤ C. ①②④ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 1.8元/千米 | 0.3元/分 | 0.8元/千米 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为行车里程7千米以内(含7千米)不收远途费,超过7千米的,超出部分每千米收0.8元. | |||
(1)小王与小张各自乘坐滴滴快车,在同一地点约见,已知到达约见地点,他们的实际行车里程分别为6千米与8.5千米,两人付给滴滴快车的乘车费相同(1)求这两辆滴滴快车的实际行车时间相差多少分钟;
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算两人各自的实际乘车时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三位数的百位上的数字减去十位上的数字等于其个位上的数字,则称这个三位数为“差数”,同时,如果百位上的数字为![]() 、十位上的数字为
、十位上的数字为![]() ,三位数
,三位数![]() 是“差数”,我们就记:
是“差数”,我们就记:![]() ,其中,
,其中,![]() ,
,![]() .例如三位数514.∵
.例如三位数514.∵![]() ,∴514是“差数”,∴
,∴514是“差数”,∴![]() .
.
(1)已知一个三位数![]() 的百位上的数字是6,若
的百位上的数字是6,若![]() 是“差数”,
是“差数”,![]() ,求
,求![]() 的值;
的值;
(2)求出小于300的所有“差数”的和,若这个和为![]() ,请判断
,请判断![]() 是不是“差数”,若是,请求出
是不是“差数”,若是,请求出![]() ;若不是,请说明理由.
;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长春创建文明城区的活动中,需铺设两段长度相等的彩色道砖,分别交给甲、乙两个施工队同时进行施工.甲、乙两队所铺设彩色道砖的长度![]() (米)与施工时间
(米)与施工时间![]() 时之间的部分函数图象如图所示.请解答下列问题:
时之间的部分函数图象如图所示.请解答下列问题:
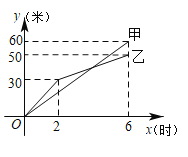
(1)甲队的速度是_______米![]() 时.
时.
(2)当![]() 时,求乙队铺设彩色道砖的长度
时,求乙队铺设彩色道砖的长度![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)如果甲队施工速度不变,乙队在开挖![]() 小时后;施工速度增加到
小时后;施工速度增加到![]() 米
米![]() 时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度.
时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的内接三角形,
的内接三角形,![]() 的角平分线
的角平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作直线
作直线![]() .
.

(1)判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若在![]() 上取一点
上取一点![]() 使
使![]() ,求证:
,求证:![]() 是
是![]() 的平分线;
的平分线;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com