
����Ŀ��Ϊ�˸��õ����ø�������ij���ί�����۾�������![]() �����ͺŵĿ��ֹ��༶ѧ��ʹ�ã���֪
�����ͺŵĿ��ֹ��༶ѧ��ʹ�ã���֪![]() �Ϳ���ÿ���۸�
�Ϳ���ÿ���۸�![]() Ԫ��
Ԫ��![]() �Ϳ���ÿ���۸��
�Ϳ���ÿ���۸��![]() ����4Ԫ��180ԪǮ�����
����4Ԫ��180ԪǮ�����![]() �Ϳ��ֱ�
�Ϳ��ֱ�![]() �Ϳ�����12����
�Ϳ�����12����
��1����![]() ��ֵ��
��ֵ��
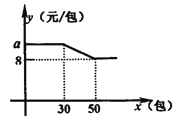
��2�������̼�Э�̣�����![]() �Ϳ��ּ۸�����Żݣ�����ÿ���۸�
�Ϳ��ּ۸�����Żݣ�����ÿ���۸�![]() ��Ԫ����������
��Ԫ����������![]() �������ĺ�����ϵ��ͼ��ʾ��
�������ĺ�����ϵ��ͼ��ʾ��![]() �Ϳ���һ�ɰ�ԭ�����ۣ�
�Ϳ���һ�ɰ�ԭ�����ۣ�
����![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
������ί��ƻ�����![]() �͡�
�͡�![]() ����100��������
����100��������![]() �Ͳ�����30�����Ҳ�����60�����ʹ���
�Ͳ�����30�����Ҳ�����60�����ʹ���![]() �Ϳ��ֶ��ٰ�ʱ��������ֵ��ܽ�����٣�����Ϊ����Ԫ��
�Ϳ��ֶ��ٰ�ʱ��������ֵ��ܽ�����٣�����Ϊ����Ԫ��
���𰸡���1��![]() ����2���ٵ�
����2���ٵ�![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ���ڵ�����
���ڵ�����![]() �Ϳ���50��ʱ��������ֵ��ܽ�����٣�����Ϊ700Ԫ
�Ϳ���50��ʱ��������ֵ��ܽ�����٣�����Ϊ700Ԫ
��������
��1�����ܼ���ÿ������=���������ݡ�180ԪǮ�����![]() �Ϳ��ֱ�
�Ϳ��ֱ�![]() �Ϳ�����12�������з�ʽ���̼�����⣻
�Ϳ�����12�������з�ʽ���̼�����⣻
��2����ͼ����Ϣ�ɵú�����ϵ�����е�![]() ʱ��
ʱ��![]() ��
��![]() ֮������һ�κ�����ϵ���ɴ���ϵ����������⣬
֮������һ�κ�����ϵ���ɴ���ϵ����������⣬
��3����![]() �Ϳ��ֹ���
�Ϳ��ֹ���![]() ����������������ۣ���
����������������ۣ���![]() ��
��![]() ʱ�����������ֵ��ܽ����
ʱ�����������ֵ��ܽ����![]() �Ϳ��ְ����ĺ�����ϵ�������ú�����������⣮
�Ϳ��ְ����ĺ�����ϵ�������ú�����������⣮
�⣺��1����������ɵã�![]() ��
��
���![]() ��
��![]() ��������
��������![]() ��
��![]() ��ԭ���̵Ľ⣬
��ԭ���̵Ľ⣬
��![]() ���������⣬��ȥ��
���������⣬��ȥ��
��![]() ��
��
��2��������ͼ����Ϣ�ã�
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��![]() ֮������һ�κ�����ϵ��
֮������һ�κ�����ϵ��
�躯������ʽΪ![]() ��ȡ��
��ȡ��![]() ��
��![]()
�����![]() �����
�����![]() ��
��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
������������![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
����![]() �Ϳ��ֹ���
�Ϳ��ֹ���![]() ������
������![]() �Ϳ���Ϊ
�Ϳ���Ϊ![]() �����������ֿ��ֵ��ܽ��Ϊ
�����������ֿ��ֵ��ܽ��Ϊ![]() Ԫ��
Ԫ��
��������![]() ��
��![]()
![]() ��
��
��![]() ʱ��
ʱ��![]() ȡ���ֵ722.5��
ȡ���ֵ722.5��
��![]() ʱ��
ʱ��![]() ȡ��Сֵ700Ԫ��
ȡ��Сֵ700Ԫ��
����![]() ʱ��
ʱ��![]() ��
��
��������![]() ʱ��������ã�
ʱ��������ã�![]() ��
��![]() ��
��![]() �����������
�����������
��![]() ��
��
���ϣ�������![]() �Ϳ���50��ʱ��������ֵ��ܽ�����٣�����Ϊ700Ԫ��
�Ϳ���50��ʱ��������ֵ��ܽ�����٣�����Ϊ700Ԫ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ԥ��ij�����з�չǰ;����1600Ԫ����һ�����ϣ����к��Ȼ����Ӧ������6000Ԫ�����������ϣ��ڶ������ϵ������ǵ�һ����3���������۱ȵ�һ����2Ԫ.
(1)��һ�����Ͻ������۶���Ԫ��
(2)�����ι������ϰ�ͬһ�۸����ۣ�����ȫ���������������1200Ԫ����ô���۵�������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҷ���ѧУ���ͥ��ͨ����Ч���������γɽ��������Ĺؼ�����ת��������Ĵ�����ij�н�������֯ȫ����Сѧ��ʦ��չ�ҷû������У������������ȡ�˲��ֽ�ʦ����������ܼҷô��������ɼ��������ݰ��ҷô����ֳ����࣬���ֱ�����������������������ͳ��ͼ��
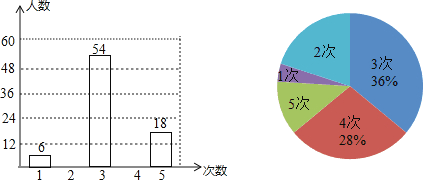
�����������Ϣ������������⣺
��1���������ͳ��ͼ����������
��2������ȡ�Ľ�ʦ�У������ܼҷô������������� ���Σ�ƽ��ÿλ��ʦ�ҷ��� ���Σ�
��3����������12000����ʦ������ƽ����ܼҷò�����3�εĽ�ʦ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
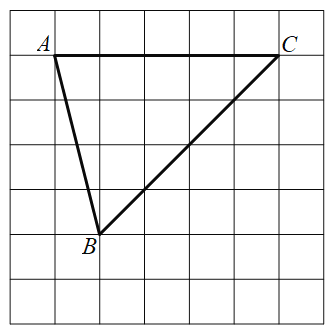
����Ŀ����ͼ���ɱ߳�Ϊ1��С�����ι��ɵ�����ÿ��С�����εĶ��������㣮![]() �Ķ����ڸ���ϣ������̶ȵ�ֱ���ڸ��������л�ͼ����ͼ���������߱�ʾ����ͼ�����ʵ�߱�ʾ������������������⣺
�Ķ����ڸ���ϣ������̶ȵ�ֱ���ڸ��������л�ͼ����ͼ���������߱�ʾ����ͼ�����ʵ�߱�ʾ������������������⣺
��1������A����BC�ĶԳƵ�F��
��2�����߶�AB����ƽ�Ƶõ��߶�DE��DE��BC���ڵ�M��ʹ![]() ��
��
��3���߶�DE�������߶�BF�Ƶ�O˳ʱ����ת![]() �ȶ��õ���B��F�Ķ�Ӧ��ֱ�ΪD��E������ͼ�л�����O
�ȶ��õ���B��F�Ķ�Ӧ��ֱ�ΪD��E������ͼ�л�����O
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
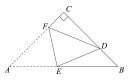
����Ŀ����ͼ���ڡ�ABC�У�AC=BC=4![]() ����C=90�㣬��D��BC�ϣ���CD=3DB������ABC�۵���ʹ��A���D�غϣ�EFΪ�ۺۣ���tan��BED��ֵ��_____��
����C=90�㣬��D��BC�ϣ���CD=3DB������ABC�۵���ʹ��A���D�غϣ�EFΪ�ۺۣ���tan��BED��ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
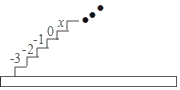
����Ŀ����ͼ������ͼ��ÿ��̨���϶�����һ���������µ��ϵĵ�1������4��̨�������α��ũ�3����2����1��0�������������ĸ�̨�������ĺͶ���ȣ�
��1��������̨���ϵ���x�Ƕ��٣�
��2����ǰ21��̨���ϵ����ĺ��Ƕ��٣�
��3�����֣�����������һ���Ĺ��ɣ���n����2�����ڵ��� ����̨���ϣ�
��4����չ�����ٻٻСͬѧһ��ֻ����1������2��̨�ף���ô���ϵ�һ��̨�ķ�����1�֣�1��1���ϵڶ���̨�ķ�����2�֣�1+1��2��2��2���ϵ�����̨�ķ�����3�֣�1+1+1��3��1+2��3��2+1��3���������ϵ����̨�ķ����������� ���֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬ�ͺŵļס�����������������ȼ�Ϻ������ʻ210km�����Ǹ��Ե�����ʻ�����ص���Զ������105km���������Ƕ���A�س�������ʻ;��ͣ�����Ӽ׳�������ȼ��Ͱ��һЩ����ȼ��ע���ҳ�������ȼ��Ͱ��Ȼ��׳�����ʻ����A�أ����ҳ�������ʻ����B�غ�����ʻ����A�أ���B����Զ�ɾ���A�أ�������
A.120kmB.140kmC.160kmD.180km
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ��������
��������![]() ��
��![]() �����һ������Ϊ
�����һ������Ϊ![]() ��
��
��1���������ߵĽ���ʽ�͵�![]() �����ꣻ
�����ꣻ
��2��![]() ��ֱ��
��ֱ��![]() �Ϸ���������һ���㣬
�Ϸ���������һ���㣬![]() ��
��![]() ��
��![]() .��
.��![]() �������
�������![]() �����ֵ�ʹ�ʱ��
�����ֵ�ʹ�ʱ��![]() �����ꣻ
�����ꣻ
��3��![]() ��
��![]() ����һ���㣬����
����һ���㣬����![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���߶�
���߶�![]() ������
������![]() ǡ�������������ϣ���ֱ��д����ʱ��
ǡ�������������ϣ���ֱ��д����ʱ��![]() �����꣮
�����꣮
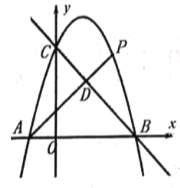
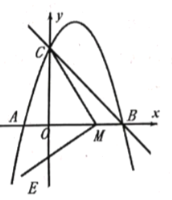
����ͼ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������̣�
��1����ͼ1���ڡ�ABC�У�DΪAB��һ�㣬��ACD����B����֤��AC2��ADAB��
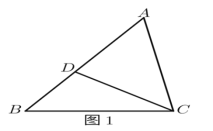
������Ӧ�ã�
��2����ͼ2����ABCD�У�EΪBC��һ�㣬FΪCD�ӳ�����һ�㣬��BFE����A����BF��4��BE��3����AD�ij���
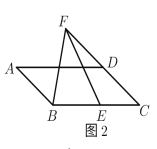
����չ��ߣ�
��3����ͼ3��������ABCD�У�E��AB��һ�㣬F�ǡ�ABC��һ�㣬EF��AC��AC��2EF����EDF��![]() ��BAD��AE��2��DF��5��������ABCD�ı߳���
��BAD��AE��2��DF��5��������ABCD�ı߳���
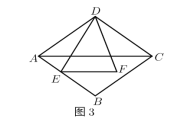
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com