
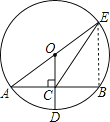
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A. 2![]() B. 8 C. 2
B. 8 C. 2![]() D. 2
D. 2![]()
【答案】C
【解析】连结BE,设⊙O的半径为R,由OD⊥AB,根据垂径定理得AC=BC=![]() AB=4,在Rt△AOC中,OA=R,OC=R-CD=R-2,根据勾股定理得到(R-2)2+42=R2,解得R=5,则OC=3,由于OC为△ABE的中位线,则BE=2OC=6,再根据圆周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可计算出CE.
AB=4,在Rt△AOC中,OA=R,OC=R-CD=R-2,根据勾股定理得到(R-2)2+42=R2,解得R=5,则OC=3,由于OC为△ABE的中位线,则BE=2OC=6,再根据圆周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可计算出CE.
解:连结BE,设⊙O的半径为R,如图所示,
∵OD⊥AB,
∴AC=BC=![]() AB=
AB=![]() ×8=4,
×8=4,
在Rt△AOC中,OA=R,OC=R-CD=R-2,
∵OC2+AC2=OA2,
∴(R-2)2+42=R2,解得R=5,
∴OC=5-2=3,
∴BE=2OC=6,
∵AE为直径,
∴∠ABE=90°,
在Rt△BCE中, ![]() .
.
考点: 1.垂径定理;2.勾股定理;3.三角形中位线定理;4.圆周角定理.
“点睛”本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:
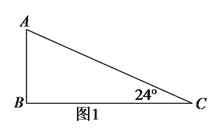
【题目】(![]() )如图
)如图![]() 中,
中,![]() ,请用直尺和圆规作一条直线,把
,请用直尺和圆规作一条直线,把![]() 分割成两个等腰三角形(不写作法,但须保留作图痕迹).
分割成两个等腰三角形(不写作法,但须保留作图痕迹).
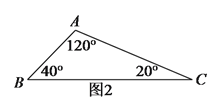
(![]() )如图
)如图![]() 中,
中,![]() 的三个内角分别为
的三个内角分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,在
,在![]() 上找一个点
上找一个点![]() ,使
,使![]() 为等腰三角形,求出
为等腰三角形,求出![]() 的长(可用含
的长(可用含![]() 的代数式表示).
的代数式表示).


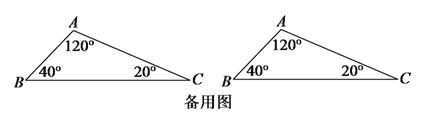
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分13分)在平面直角坐标系中,O为原点,直线y =-2x-1与y轴交于点A,与直线y =-x交于点B,点B关于原点的对称点为点C.

(1)求过A,B,C三点的抛物线的解析式;
(2)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②若点P的横坐标为t(-1<t<1),当t为何值时,四边形PBQC面积最大,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明锻炼健身,从A地匀速步行到B地用时25分钟.若返回时,发现走一小路可使A、B两地间路程缩短200米,便抄小路以原速返回,结果比去时少用2.5分钟.
(1)求返回时A、B两地间的路程;
(2)若小明从A地步行到B地后,以跑步形式继续前进到C地(整个锻炼过程不休息).据测试,在他整个锻炼过程的前30分钟(含第30分钟),步行平均每分钟消耗热量6卡路里,跑步平均每分钟消耗热量10卡路里;锻炼超过30分钟后,每多跑步1分钟,多跑的总时间内平均每分钟消耗的热量就增加1卡路里.测试结果,在整个锻炼过程中小明共消耗904卡路里热量.问:小明从A地到C地共锻炼多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是 (只需填序号即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
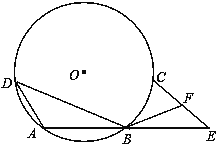
【题目】(10分)如图,已知⊙O上依次有A、B、C、D四个点,![]() =
=![]() ,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
(1)求证:BF=![]() BD;
BD;
(2)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com