
分析 (1)根据负整数指数幂和有理数的除法和减法可以解答本题;
(2)根据分式的加法和乘法可以解答本题.
解答 解:(1)(-1)5-${(\frac{1}{3})}^{-2}$÷(-3)-${({2\sqrt{3}})^2}$
=-1-9÷(-3)-12
=-1+3-12
=-10;
(2)($\frac{{b}^{2}}{{a}^{2}{-b}^{2}}$+1)•$\frac{{a}^{2}+2ab{+b}^{2}}{{a}^{2}}$
=$\frac{a^2}{{{a^2}-{b^2}}}•\frac{{{a^2}+2ab+{b^2}}}{a^2}$
=$\frac{a^2}{{({a+b})({a-b})}}•\frac{{{{({a+b})}^2}}}{a^2}$
=$\frac{a+b}{a-b}$.
点评 本题考查分式的混合运算、实数的运算、负整数指数幂,解答本题的关键是明确它们各自的计算方法.


科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2:3 | B. | 4:16 | C. | 3:2 | D. | 16:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是AC=BD.(写一种即可)
如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是AC=BD.(写一种即可)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
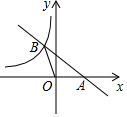 如图,直线y=-$\frac{1}{2}$x+b与x轴交于点A,与双曲线y=-$\frac{4}{x}$(x<0)交于点B,若S△AOB=2,则b的值是( )
如图,直线y=-$\frac{1}{2}$x+b与x轴交于点A,与双曲线y=-$\frac{4}{x}$(x<0)交于点B,若S△AOB=2,则b的值是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com