
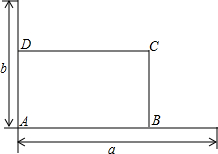
 ������У�Ļ�У�ij��ѧ��ȤС���ͬѧ���ó�Ϊ16m����ʣ��������滥�ഹֱ��ǽ��a��bΧһ�����λ���ABCD��ǽ��a��b�������ó���Ϊ14m��9m�����軨��AB�ߵij�Ϊx m�����ΪS m2
������У�Ļ�У�ij��ѧ��ȤС���ͬѧ���ó�Ϊ16m����ʣ��������滥�ഹֱ��ǽ��a��bΧһ�����λ���ABCD��ǽ��a��b�������ó���Ϊ14m��9m�����軨��AB�ߵij�Ϊx m�����ΪS m2���� ��1����������ó�������=����������ó�S��x֮��ĺ�����ϵʽ��
��2����������ó�������=39���ⷽ�̼��ɣ�
��2�����ݣ�1���к�������ʽ�������ö��κ��������������ֵ��
��� �⣺��1���軨��AB�ߵij�Ϊx m�����ΪS m2
S=x��16-x��=-x2+16x��7��x��14����
��2�����������з��̵ã�
-x2+16x=39
��ã�x1=13��x2=3����ȥ��
��x=13ʱ��16-x=3��
��Χ�ɵľ��λ������Ϊ39m2����ʱ���Եij�����ֱ�Ϊ13m��3m��
��3��S=-x2+16x=-��x-8��2+64
��AB�ij�Ϊ8mʱ��Χ�ɵľ��λ�����������������64m2��
���� ������Ҫ�����˶��κ�����Ӧ���Լ����κ�����ֵ���ó�S��x�ĺ�����ϵʽ�ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
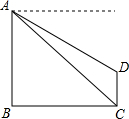 С���ڵ������ϸ߶�Ϊ450��A������ô�¥CD¥��D�ĸ���30�㣬С���ڴ�¥¥��C�����A��������Ϊ45�㣮
С���ڵ������ϸ߶�Ϊ450��A������ô�¥CD¥��D�ĸ���30�㣬С���ڴ�¥¥��C�����A��������Ϊ45�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
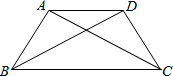 ��ͼ��������ABCD�У�AD��BC��AB=AD=CD��BD=BC�����ABC�Ķ�����
��ͼ��������ABCD�У�AD��BC��AB=AD=CD��BD=BC�����ABC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
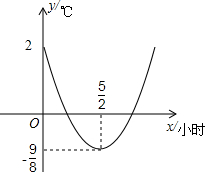 ij������һ��ֲ��������0�����³���ʱ�䳬��2.5Сʱ������˪���ֺ������ȡԤ����ʩ����ͼ������̨ij�췢���ĸõ���������Ϣ��Ԥ���˴���0ʱ��5ʱ������ʱ��仯�����������ʱ��Ķ��κ���������ͼ���㣨0��2�����䶥�������ǣ�$\frac{5}{2}$��-$\frac{9}{8}$�����������ͼ����Ϣ�ж�����ֲ������Ƿ���Ҫ��ȡ������ʩ����˵�����ɣ�
ij������һ��ֲ��������0�����³���ʱ�䳬��2.5Сʱ������˪���ֺ������ȡԤ����ʩ����ͼ������̨ij�췢���ĸõ���������Ϣ��Ԥ���˴���0ʱ��5ʱ������ʱ��仯�����������ʱ��Ķ��κ���������ͼ���㣨0��2�����䶥�������ǣ�$\frac{5}{2}$��-$\frac{9}{8}$�����������ͼ����Ϣ�ж�����ֲ������Ƿ���Ҫ��ȡ������ʩ����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ��n-1��ö���� | B�� | nö���� | C�� | ��n+1��ö���� | D�� | ��3n-2��ö���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪ʵ��a��b��c������������Ӧ�ĵ���ͼ��ʾ��������и��⣮
��֪ʵ��a��b��c������������Ӧ�ĵ���ͼ��ʾ��������и��⣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
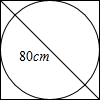 ��ͼ��ľ��С����ӶԽ��߳�Ϊ80cm��������ľ���Ͻ���һ�����Ķ����������Բ��ֱ���Ƕ��٣�
��ͼ��ľ��С����ӶԽ��߳�Ϊ80cm��������ľ���Ͻ���һ�����Ķ����������Բ��ֱ���Ƕ��٣��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com