
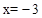 ���������ཻ�ڵ������ĵ�M����x���ཻ�ڵ�N����
���������ཻ�ڵ������ĵ�M����x���ཻ�ڵ�N���� ��
��
 ��������
�������� ��x�����һ����ΪA��BΪ������
��x�����һ����ΪA��BΪ������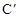 �Ϻ�����Ϊ2�ĵ㡣
�Ϻ�����Ϊ2�ĵ㡣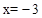 ����ON=3��
����ON=3�� ����NM=9����M����3����9����
����NM=9����M����3����9���� ��
��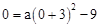 ����
���� ��
�� ����
���� ��
��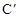 ��������C��ԭ��O��ת1800�õ���
��������C��ԭ��O��ת1800�õ���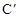 ��������C����ԭ��O�Գơ���������
��������C����ԭ��O�Գơ���������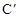 �Ķ�������Ϊ��3��9����
�Ķ�������Ϊ��3��9����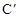 �Ľ���ʽΪ
�Ľ���ʽΪ ����
����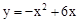 ��
��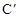 �Ϻ�����Ϊ2�ĵ㣬����x=2����y=8����B��2��8����
�Ϻ�����Ϊ2�ĵ㣬����x=2����y=8����B��2��8���� ����ã�
����ã�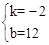 ��
�� ��
�� ��
�� ��
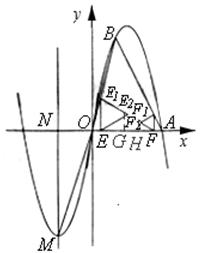
��
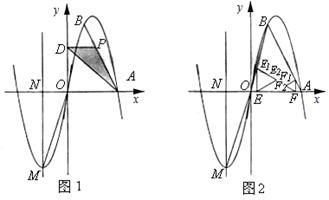
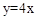 ���ɢ�ֱ��AB��
���ɢ�ֱ��AB�� ��
�� ʱ��E1��OB�ϣ�F1��AB�ϣ�
ʱ��E1��OB�ϣ�F1��AB�ϣ�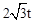 ��OG=
��OG= ��GE2=2t��
��GE2=2t��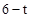 ��FF1=2t��HF=
��FF1=2t��HF= ��OH=
��OH= ��HF2= t��
��HF2= t�� ��2t����F��6��t��0����F1��
��2t����F��6��t��0����F1��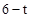 ��2t����F2��
��2t����F2�� ��t����
��t���� ��
��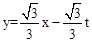 ����F1��
����F1��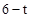 ��2t�����룬��
��2t�����룬��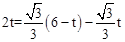 �����
�����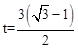 ��
�� ����F��
����F��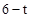 ��0�����룬��
��0�����룬�� ��
��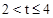 ʱ��E1��F1����AB�ϣ�
ʱ��E1��F1����AB�ϣ�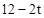 ��EG=
��EG= ��OG=
��OG=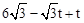 ��GE2=
��GE2=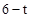 ��
��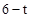 ��FF1=2t��HF=
��FF1=2t��HF= ��OH=
��OH= ��HF2= t��
��HF2= t��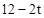 ����E2��
����E2��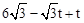 ��
��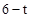 ����F��
����F��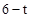 ��0����F1��
��0����F1��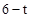 ��2t����F2��
��2t����F2�� ��t����
��t����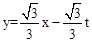 ����F1��
����F1��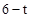 ��2t�����룬��
��2t�����룬��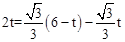 �����
�����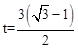 ��������
��������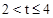 ��
�� ʱ��ͬһֱ���ϣ��ʵ�
ʱ��ͬһֱ���ϣ��ʵ�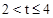 ʱE1E2��FF2��������ͬһֱ���ϡ�
ʱE1E2��FF2��������ͬһֱ���ϡ�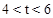 ʱ�����������۵Ľ������AE1E2��һ�����AF1F2��ijһ�߲�������ͬһֱ���ϡ�
ʱ�����������۵Ľ������AE1E2��һ�����AF1F2��ijһ�߲�������ͬһֱ���ϡ�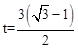 ��
�� ��t=3��
��t=3�� �������M�����꣬���ô���ϵ����������κ�������ʽ���ɡ�
�������M�����꣬���ô���ϵ����������κ�������ʽ���ɡ� ��
��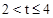 ��
��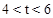 ����������ۣ�ÿ������ַ�EE1��FF1��ͬһֱ���ϣ�EE2��F1F2��ͬһֱ�ߺ�E1E2��FF2��ͬһֱ��������������ۡ�
����������ۣ�ÿ������ַ�EE1��FF1��ͬһֱ���ϣ�EE2��F1F2��ͬһֱ�ߺ�E1E2��FF2��ͬһֱ��������������ۡ�

 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
�ٶ� (ǧ��/ʱ) (ǧ��/ʱ) | 0 | 5 | 10 | 15 | 20 | 25 | �� |
ɲ������ (��) (��) | 0 |  | 2 |  | 6 |  | �� |
 ��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������
��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������ (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
(ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
 (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)���㺯��
(ǧ��/ʱ)���㺯�� ������������ٶȷ��������ײԭ��
������������ٶȷ��������ײԭ�� �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ������������C1����ƽ��h����λ��h��0���õ�������C2��һ��ƽ����x���ֱ�������������߽���A��B��C��D�ĵ㣨��ͼ�����ҵ�A��C����y��Գƣ�ֱ��AB��x��ľ�����m2��m��0����
������������C1����ƽ��h����λ��h��0���õ�������C2��һ��ƽ����x���ֱ�������������߽���A��B��C��D�ĵ㣨��ͼ�����ҵ�A��C����y��Գƣ�ֱ��AB��x��ľ�����m2��m��0����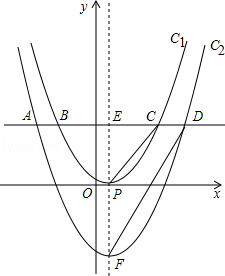
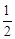 ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
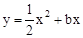 ��ֱ��
��ֱ��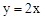 ���ڵ�O��0��0����
���ڵ�O��0��0����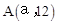 ����B����������O��A֮���һ�����㣬����B�ֱ������ᡢ�����ƽ������ֱ��OA���ڵ�C��E��
����B����������O��A֮���һ�����㣬����B�ֱ������ᡢ�����ƽ������ֱ��OA���ڵ�C��E��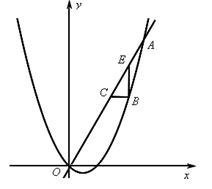
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 �У���OΪԭ�㣬��B�ڷ���������
�У���OΪԭ�㣬��B�ڷ��������� ��
�� ��
�� ��ͼ���ϣ���BOC�����Ϊ
��ͼ���ϣ���BOC�����Ϊ ��
��
 �Ĺ�ϵʽ��
�Ĺ�ϵʽ��  ����λ���ٶ��˶���������һ�����㵽��˵�ʱ����һ��������ֹ֮ͣ�˶������˶�ʱ����t��ʾ����BEF�������
����λ���ٶ��˶���������һ�����㵽��˵�ʱ����һ��������ֹ֮ͣ�˶������˶�ʱ����t��ʾ����BEF������� ��ʾ�����S����t�ĺ�����ϵʽ����������˶�ʱ��tȡ��ֵʱ����BEF��������
��ʾ�����S����t�ĺ�����ϵʽ����������˶�ʱ��tȡ��ֵʱ����BEF��������  ��ʱ�������������Ƿ���ڵ�P��ʹ��PEF���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��ʱ�������������Ƿ���ڵ�P��ʹ��PEF���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
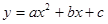 ��ͼ����ͼ��ʾ�������н��ۣ�
��ͼ����ͼ��ʾ�������н��ۣ�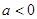 ����
����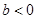 ����
����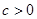 ����
���� 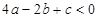 ����
����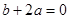
| A��1�� | B��2�� | C��3�� | D��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com