
【题目】如图,已知矩形ABCD,点E为BC的中点,将△ABE沿直线AE折叠,点B落在B′点处,连接B′C

(1)求证:AE∥B′C;
(2)若AB=4,BC=6,求线段B′C的长。
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)过E作EH⊥CF于H,由折叠的性质和点E是BC的中点以及矩形的性质可得△ABE∽△EHC,进而求得∠AEB=∠ECH,最后可得AE∥B′C;
(2)由(1)中的△ABE∽△EHC,即可求得线段B′C的长.
试题解析:

(1)证明:解:过E作EH⊥CF于H,
由折叠的性质得:BE=EF,∠BEA=∠FEA,
∵点E是BC的中点,
∴CE=BE,
∴EB′=CE,
∴∠B′EH=∠CEH,
∴∠AEB+∠CEH=90°,
在矩形ABCD中,
∵∠B=90°,
∴∠BAE+∠BEA=90°,
∴∠BAE=∠CEH,∠B=∠EHC,
∴△ABE∽△EHC,
∴∠AEB=∠ECH,
∴AE∥B′C;
(2)解:∵△ABE∽△EHC,
∴![]() ,
,
∴HC=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B′C′的位似比;
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了右图,如果继续“生长”下去 ,它将变得“枝繁叶茂”,请你算出“生长”了2018次后形成的图形中所有的正方形的面积和是( )

A. 2017 B. 2018 C. 2019 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P , 若EF=2,则梯形ABCD的周长为( ) 
A.12
B.10
C.8
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梯形ABCD中AD∥BC , E是AB的中点,过E作两底的平行线交DC于F , 则下面结论错误的是( )
A.EF平分线段AC
B.梯形上下底间任意两点的连线段被EF平分
C.梯形EBCF与梯形AEFD周长之差的绝对值等于梯形两底之差的绝对值
D.梯形EBCF的面积比梯形AEFD的面积大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只给定三角形的两个元素,画出的三角形的形状和大小是不确定的,在下列给定的两个条件上增加一个“AB=5cm”的条件后,所画出的三角形的形状和大小仍不能完全确定的是( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形,矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.设菱形相邻两个内角的度数分别为m和n , 将菱形的“接近度”定义为|m-n|,于是,|m-n|越小,菱形越接近于正方形.若菱形的一个内角为70°,则该菱形的“接近度”等于;当菱形的“接近度”等于时,菱形是正方形.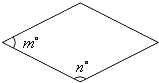
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( ) 
A.函数有最小值
B.对称轴是直线x= ![]()
C.当x< ![]() ,y随x的增大而减小
,y随x的增大而减小
D.当﹣1<x<2时,y>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com