
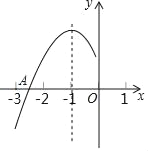
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2<﹣1,则y1>y2,⑤abc>0.其中正确结论的个数是( )
A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
【解析】①∵抛物线与x轴有两个交点,
∴△=b2﹣4ac>0,
∴4ac﹣b2<0,结论①正确;
②∵抛物线的对称轴为直线x=﹣1,
∴﹣![]() =﹣1,
=﹣1,
∴b=2a,即2a﹣b=0,结论②正确;
③∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,
∴当x=1与x=﹣3的值相等,即当x=1时y<0,
∴a+b+c<0,结论③正确;
④∵当x<﹣1时,y随x的增大而增大,x1<x2<﹣1,
∴y1<y2,结论④错误;
⑤∵抛物线开口向下,对称轴为直线x=﹣1,与y轴交于正半轴,
∴a<0,b=2a<0,c>0,
∴abc>0,结论⑤正确,
故选B.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】华联超市购进一批四阶魔方,按进价提高40%后标价,为了让利于民,增加销量,超市决定打八折出售,这时每个魔方的售价为28元.
(1)求魔方的进价?
(2)超市卖出一半后,正好赶上双十一促销,商店决定将剩下的魔方以每3个80元的价格出售,很快销售一空,这批魔方超市共获利2800元,求该超市共购进魔方多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)a、b为有理数,且a+b、a﹣b在数轴上如图所示:
![]()
①判断:a 0,b 0,a b(用“>”“<”“=”填空).
②若x=|2a+b|﹣3|b|﹣|3﹣2a|+2|b﹣1|,求(2x2-![]() +3x)﹣4(x﹣x2+
+3x)﹣4(x﹣x2+![]() )的值;
)的值;
(2)若c为有理数,![]() ,且ab﹣bc+ac=﹣99,求(3a﹣4b+2c)2+
,且ab﹣bc+ac=﹣99,求(3a﹣4b+2c)2+![]() abc的值.
abc的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=
的图象与一次函数y2=![]() 的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=
的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=![]() 的图象上.
的图象上.
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新规定这样一种运算法则:a△b=![]() ,如2△3=
,如2△3=![]() -2×3=4-6=-2;
-2×3=4-6=-2;
利用运算法则解决下列问题:
(1)1△2= ,(-1)△[1△(-1)] = .
(2)若2△x=3,求x的值.
(3)若(-2)△x=-2+x,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
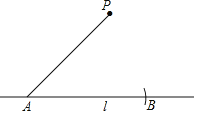
【题目】在数学课上,老师提出如下问题:如何使用尺规完成“过直线l外一点P作已知直线l的平行线”.
小明的作法如下:
①在直线l上取一点A,以点A为圆心,AP长为半径作弧,交直线l于点B;
②分别以P,B为圆心,以AP长为半径作弧,两弧相交于点Q(与点A不重合);
③作直线PQ.所以直线PQ就是所求作的直线.根据小明的作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB=AP= = .
∴四边形ABQP是菱形( )(填推理的依据).
∴PQ∥l.
查看答案和解析>>
科目:初中数学 来源: 题型:
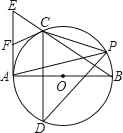
【题目】如图,Rt△ABE中,AB⊥AE以AB为直径作⊙O,交BE于C,弦CD⊥AB,F为AE上一点,连FC,则FC=FE
(1)求证:CF是⊙O的切线;
(2)已知点P为⊙O上一点,且tan∠APD=![]() ,连CP,求sin∠CPD的值.
,连CP,求sin∠CPD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com