
如图,在等腰Rt△ABC与等腰Rt△DBE中,∠BDE=∠ACB=90°,且BE在AB边上,取AE的中点F,CD的中点G,连结GF.
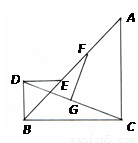
(1)FG与DC的位置关系是 ,FG与DC的数量关系是 ;
(2)若将△BDE绕B点逆时针旋转180°,其它条件不变,请完成下图,并判断(1)中的结论是否仍然成立? 请证明你的结论.
(1)FG⊥CD ,FG=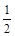 CD;(2)成立
CD;(2)成立
【解析】
试题分析:(1)延长ED交AC的延长线于M,连接FC、FD、FM,根据矩形的性质可得CM=BD,根据等腰直角三角形的性质可得ED=BD=CM,再结合∠E=∠A=45º可证得△AEM是等腰直角三角形,由F是AE的中点可证得MF⊥AE,EF=MF,∠E=∠FMC=45º,即可证得△EFD≌△MFC,则可得FD=FC,∠EFD=∠MFC,又∠EFD+∠DFM=90º即得∠MFC+∠DFM=90º,即可得到△CDF是等腰直角三角形,从而可以证得结论;
(2)证法同(1).
解:(1)FG⊥CD ,FG=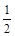 CD;
CD;
(2)延长ED交AC的延长线于M,连接FC、FD、FM

∴四边形 BCMD是矩形.
∴CM=BD.
又△ABC和△BDE都是等腰直角三角形.
∴ED=BD=CM.
∵∠E=∠A=45º
∴△AEM是等腰直角三角形.
又F是AE的中点.
∴MF⊥AE,EF=MF,∠E=∠FMC=45º.
∴△EFD≌△MFC.
∴FD=FC,∠EFD=∠MFC.
又∠EFD+∠DFM=90º
∴∠MFC+∠DFM=90º
即△CDF是等腰直角三角形.
又G是CD的中点.
∴FG=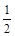 CD,FG⊥CD.
CD,FG⊥CD.
考点:旋转问题的综合题
点评:此类问题难度较大,在中考中比较常见,一般在压轴题中出现,需特别注意.


科目:初中数学 来源: 题型:
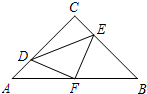 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:| A、①②③ | B、①④⑤ | C、①③④ | D、③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:
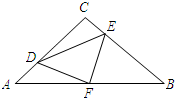 上运动,且保持AD=CE.连接DE、DF、EF.
上运动,且保持AD=CE.连接DE、DF、EF.查看答案和解析>>
科目:初中数学 来源: 题型:
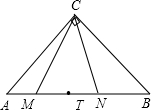 如图,在等腰Rt△ABC中,∠ACB=90°,CA=CB,点M、N是AB上任意两点,且∠MCN=45°,点T为AB的中点.以下结论:①AB=
如图,在等腰Rt△ABC中,∠ACB=90°,CA=CB,点M、N是AB上任意两点,且∠MCN=45°,点T为AB的中点.以下结论:①AB=| 2 |
| A、①②③④ | B、只有①②③ |
| C、只有①③④ | D、只有②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在等腰Rt△ABC中,∠C=90°,AC=8
如图,在等腰Rt△ABC中,∠C=90°,AC=8| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com