
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
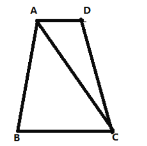
(1)求线段![]() 的长;
的长;
(2)联结![]() ,交对角线
,交对角线![]() 于点
于点![]() ,求
,求![]() 的余切值.
的余切值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)作BE垂直AC于E,由BC求出BE的长,再根据BE的长求出AE的长,即可求出AC的长.
(2)由题意做OP垂直BC于P,根据三角形相似,求出OC的长,再根据![]() 求出OP,PC即可求出∠OBC的余切,即
求出OP,PC即可求出∠OBC的余切,即![]() 的余切值.
的余切值.
(1)
作BE垂直AC于E,
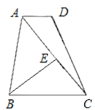
∵![]() ,BC=5,
,BC=5,
∴EC=3,
由勾股定理可得:BE=4,
∵∠BAC=45°,
∴AE=BE,
∴AE=4,
∴AC=AE+EC=4+3=7,
即AC的长为7,
由BC求出BE的长,再根据BE的长求出AE的长,即可求出AC的长.
(2)
由题意作图,
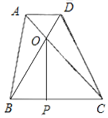
∵AD‖BC,
∴∠OBC=∠ADO,
∴AO:OC=AD:BC(平行线分线段成比例),
∴AO:OC=2:5,
∵AC=7,
∴OC=5,
做OP垂直BC于P,
∵![]() ,
,
∴PC=3,
由勾股定理可得:OP=4,
∵BC=5,
∴BP=2,
∴![]() 的余切值为
的余切值为![]() =
=![]() =
=![]() ,
,
即![]() 的余切值为
的余切值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,点C、E是⊙O上的两点,CE=CB,![]() ,延长AE交BC的延长线于点F.
,延长AE交BC的延长线于点F.

(1)求证:CD是⊙O的切线;
(2)求证:CE=CF
(3)若BD=1,![]() ,求直径AB的长.
,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点![]() 到
到![]() 的三个顶点的距离分别为
的三个顶点的距离分别为![]() 、
、![]() 、
、![]() ,若有
,若有![]() ,则称点
,则称点![]() 为
为![]() 关于点
关于点![]() 的勾股点.
的勾股点.
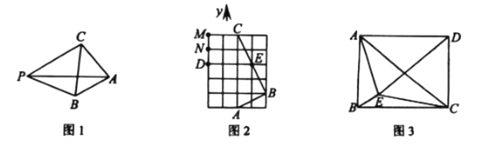
(1)如图2,在![]() 的网格中,每个小正方形的边长均为1,点
的网格中,每个小正方形的边长均为1,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均在小正方形的顶点上,则点E是
均在小正方形的顶点上,则点E是![]() 关于点B的勾股点.
关于点B的勾股点.
(2)如图3,![]() 是矩形
是矩形![]() 内一点,且点
内一点,且点![]() 是
是![]() 关于点
关于点![]() 的勾股点,
的勾股点,
①求证:![]() ;
;
②若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
(3)如图3,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是矩形
是矩形![]() 内一点,且点
内一点,且点![]() 是
是![]() 关于点
关于点![]() 的勾股点.
的勾股点.
①当![]() 时,求
时,求![]() 的长;
的长;
②直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
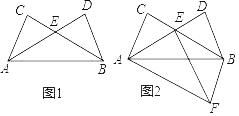
【题目】如图1,点C、D是线段AB同侧两点,且AC=BD,∠CAB=∠DBA,连接BC,AD交于点 E.
(1)求证:AE=BE;
(2)如图2,△ABF与△ABD关于直线AB对称,连接EF.
①判断四边形ACBF的形状,并说明理由;
②若∠DAB=30°,AE=5,DE=3,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
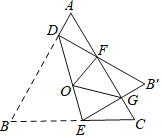
A. △ADF≌△CGE
B. △B′FG的周长是一个定值
C. 四边形FOEC的面积是一个定值
D. 四边形OGB'F的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
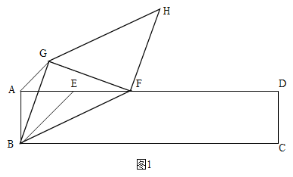
【题目】如图,矩形ABCD,AB=2,BC=10,点E为AD上一点,且AE=AB,点F从点E出发,向终点D运动,速度为1cm/s,以BF为斜边在BF上方作等腰直角△BFG,以BG,BF为邻边作BFHG,连接AG.设点F的运动时间为t秒.
(1)试说明:△ABG∽△EBF;
(2)当点H落在直线CD上时,求t 的值;
(3)点F从E运动到D的过程中,直接写出HC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
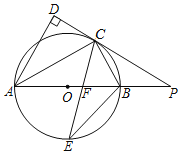
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AC平分∠DAB,直线DC与AB的延长线相交于点P,AD与PC延长线垂直,垂足为点D,CE平分∠ACB,交AB于点F,交⊙O于点E.
(1)求证:PC与⊙O相切;
(2)求证:PC=PF;
(3)若AC=8,tan∠ABC=![]() ,求线段BE的长.
,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
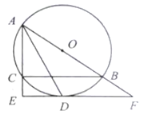
【题目】如图所示,![]() 是
是![]() 的外接圆,
的外接圆,![]() 为直径,
为直径,![]() 的平分线交O于点D,过点D作
的平分线交O于点D,过点D作![]() ,分别交
,分别交![]() ,
,![]() 的延长线于点E,F.
的延长线于点E,F.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)填空:
①当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 为菱形;
为菱形;
②若![]() 的半径为
的半径为![]() ,
,![]() ,则
,则![]() 的长为_________.
的长为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com