
【题目】如图,点A在∠O的一边OA上.按要求画图并填空:

(1)过点A画直线AB ⊥OA,与∠O的另一边相交于点B;
(2)过点A画OB的垂线段AC,垂足为点C;
(3)过点C画直线CD∥OA ,交直线AB于点D;
(4)∠CDB= °;
(5)如果OA=8,AB=6,OB=10,则点A到直线OB的距离为 .
科目:初中数学 来源: 题型:
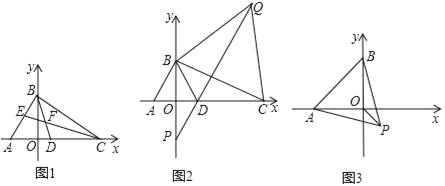
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图直线![]() 的解析式为y=x+1,直线
的解析式为y=x+1,直线![]() 的解析式为
的解析式为![]() ;这两个图象交于y轴上一点C,直线
;这两个图象交于y轴上一点C,直线![]() 与x轴的交点B(2,0).
与x轴的交点B(2,0).
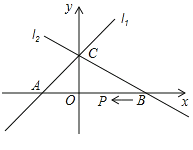
(1)求a、b的值;
(2)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样规格的黑白两种颜色的正方形,按如图①的方式拼图,请根据图中的信息完成下列的问题

(1)在图②中用了___________块黑色正方形,在图③中用了_____________块黑色正方形;
(2)按如图的规律继续铺下去,那么第![]() 个图形要用____________块黑色正方形;
个图形要用____________块黑色正方形;
(3)如果有足够多的白色正方形,能不能恰好用完![]() 块黑色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
块黑色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
求证:∠EGF=90°
证明:∵HG∥AB(已知)
∴∠1=∠3(__________________________)
又∵HG∥CD(已知)
∴∠2=∠4(_______________________________)
∵AB∥CD(已知)
∴∠BEF+___________=180°(_____________________)
又∵EG平分∠BEF,FG平分∠EFD (已知)
∴∠1=(______)∠BEF,∠2=(______)∠EFD (______________________)
∴∠1+∠2=(________) (∠BEF +∠EFD)=(____________)
∴∠3+∠4=90°(_______________________)即∠EGF=90°

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7)、(-3,0)、(0,3).
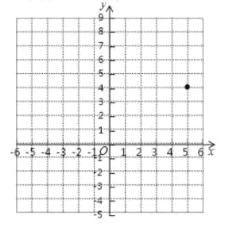
(1)画出△ABC,并求△ABC的面积.
(2)在平面直角坐标系中平移△ABC,使点C经过平移后的对应点为C'(5,4),平移后△ABC得到△A'B'C',画出平移后的△A'B'C',并写出点A',B'的坐标
(3)P(-3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,-3),则m= n=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图①,若AB∥ON,则
①∠ABO的度数是________.
②当∠BAD=∠ABD时,x=________;当∠BAD=∠BDA时,x=________.
(2)如图②,若AB⊥OM,则是否存在这样的x值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
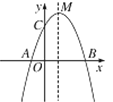
【题目】如图,已知抛物线y=-x2+bx+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,3).
(1)求抛物线的解析式及顶点M的坐标;
(2)在抛物线的对称轴上找到点P,使得△PAC的周长最小,并求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线 y=kx+b 与直线![]() 交点的纵坐标为 5,而与直线 y=3x﹣9 的交点的横 坐标也是 5,则直线 y=kx+b 与两坐标轴围成的三角形面积为( )
交点的纵坐标为 5,而与直线 y=3x﹣9 的交点的横 坐标也是 5,则直线 y=kx+b 与两坐标轴围成的三角形面积为( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com