
【题目】阅读以下材料,并按要求完成相应的任务.
“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题:今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?用现在的数学语言表达是:如图,![]() 为
为![]() 的直径,弦
的直径,弦![]() ,垂足为
,垂足为![]() ,
,![]() 寸,
寸,![]() 尺,其中1尺
尺,其中1尺![]() 寸,求出直径
寸,求出直径![]() 的长.
的长.
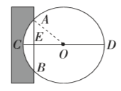
解题过程如下:
连接![]() ,设
,设![]() 寸,则
寸,则![]() 寸.
寸.
∵![]() 尺,∴
尺,∴![]() 寸.
寸.
在![]() 中,
中,![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() 寸.
寸.
任务:
(1)上述解题过程运用了 定理和 定理.
(2)若原题改为已知![]() 寸,
寸,![]() 尺,请根据上述解题思路,求直径
尺,请根据上述解题思路,求直径![]() 的长.
的长.
(3)若继续往下锯,当锯到![]() 时,弦
时,弦![]() 所对圆周角的度数为 .
所对圆周角的度数为 .
【答案】(1)垂径,勾股;(2)26寸;(3)![]() 或
或![]()
【解析】
(1)由解题过程可知根据垂径定理求出AE的长,在Rt△OAE中根据勾股定理求出r的值,即可得到答案.
(2)连接OA,设OA=r寸,则OE=DE-r=25-r,再根据垂径定理求出AE的长,在Rt△OAE中根据勾股定理求出r的值,进而得出结论.
(3)当AE=OE时,△AEO是等腰直角三角形,则∠AOE=45°,∠AOB=90°,所以由圆周角定理推知弦AB所对圆周角的度数为 45°或135°.
解:(1)根据题意知,上述解题过程运用了 垂径定理和 勾股定理.
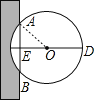
故答案是:垂径;勾股;
(2)连接OA,设OA=r寸,则OE=DE-r=(25-r)寸
∵AB⊥CD,AB=1尺,∴AE=![]() AB=5寸
AB=5寸
在Rt△OAE中,OA2=AE2+OE2,即r2=52+(25-r)2,解得r=13,
∴CD=2r=26寸
(2)∵AB⊥CD,
∴当AE=OE时,△AEO是等腰直角三角形,
∴∠AOE=45°,
∴∠AOB=2∠AOE=90°,
∴弦AB所对圆周角的度数为![]() ∠AOB=45°.
∠AOB=45°.
同理,优弧AB所对圆周角的度数为135°.
故答案是:45°或135°.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
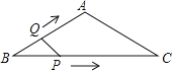
【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以![]() cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发以2cm/s的速度沿B→A→C运动到点C停止.若△BPQ的面积为y运动时间为x(s),则下列图象中能大致反映y与x之间关系的是( )
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发以2cm/s的速度沿B→A→C运动到点C停止.若△BPQ的面积为y运动时间为x(s),则下列图象中能大致反映y与x之间关系的是( )
A.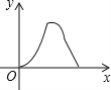 B.
B.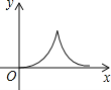 C.
C.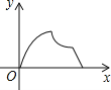 D.
D.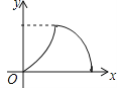
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(m+1)x2﹣2x﹣1=0有两个不相等的实数根,
(1)求m的取值范围;
(2)若x=1是方程的一个根,求m的值和另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
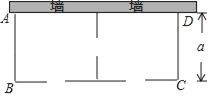
【题目】某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米.
(1)饲养场的长为多少米(用含a的代数式表示).
(2)若饲养场的面积为288m2,求a的值.
(3)当a为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
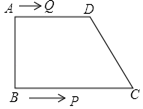
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度向
的速度向![]() 点运动,
点运动,![]() 、
、![]() 两点同时出发,其中一点到达终点时另一点也停止运动.若
两点同时出发,其中一点到达终点时另一点也停止运动.若![]() ,当
,当![]() __
__![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点D是△ABC中AC的中点,AE∥BC,ED交AB于点G,交BC的延长线于点F.
(1)求证:△GAE∽△GBF;
(2)求证:AE=CF;
(3)若BG:GA=3:1,BC=8,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
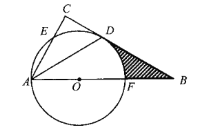
【题目】如图,在![]() 中,
中,![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 为半径的圆恰好经过点
为半径的圆恰好经过点![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]()
(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)若![]() ,
,![]() ,求阴影部分的面积(结果保留
,求阴影部分的面积(结果保留![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com