
【题目】下列命题中,正确的是( )
A. 两个相似三角形面积比为2:3,则周长比是4:9
B. 相似图形一定构成位似图形
C. 如果点D、E分别在△ABC的边AB、AC上,△ABC与△ADE相似,则DE∥BC
D. 在Rt△ABC中,斜边上的高CD2=ADBD
【答案】D
【解析】
两个相似三角形面积比为2:3,则周长比是![]() :
:![]() ;
;
相似图形不一定构成位似图形,但位似图形是相似图形;
如果点D、E分别在△ABC的边AB、AC上,△ABC与△ADE相似,则可能DE∥BC或AD:AC=AE:AB,即将图形反转相似;
在Rt△ABC中,斜边上的高CD2=ADBD.所以正确的是D.
解:A、两个相似三角形面积比为2:3,则周长比是![]() :
:![]() ;
;
B、相似图形不一定构成位似图形,但位似图形是相似图形;
C、如果点D、E分别在△ABC的边AB、AC上,△ABC与△ADE相似,则可能DE∥BC或AD:AC=AE:AB,即将图形反转相似;
D、如图: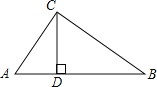
∵CD⊥AB,∠ACB=90°
∴∠ADC=∠BDC=90°
∴∠A+∠ACD=90°,∠A+∠B=90°
∴∠ACD=∠B
∴△ACD∽△CBD
∴AD:CD=CD:BD
∴CD2=ADBD
故选:D.


科目:初中数学 来源: 题型:
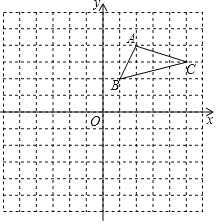
【题目】在如图所示的方格纸(每个小方格都是边长为1个单位的正方形)中建立平面直角坐标系,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点B1的坐标;
(2)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和x)
查看答案和解析>>
科目:初中数学 来源: 题型:
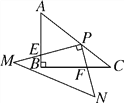
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中记录了一次试验中时间与温度的数据(假设温度的变化是均匀的)
时间(min) | 0 | 5 | 10 | 15 | 20 | 25 |
温度(℃) | 10 | 25 | 40 | 55 | 70 | 85 |
(1)用文字概述温度与时间之间的关系:______;
(2)21min的温度是多少?请列算式计算;
(3)什么时间的温度是34℃?请用方程求解.
查看答案和解析>>
科目:初中数学 来源: 题型:
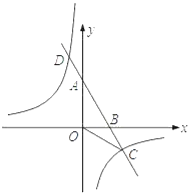
【题目】如图,已知A、B两点的坐标分别为A(0,2![]() ),B(2,0),直线AB与反比例函数y=
),B(2,0),直线AB与反比例函数y=![]() 的图象交于点C和点D(﹣1,a).
的图象交于点C和点D(﹣1,a).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
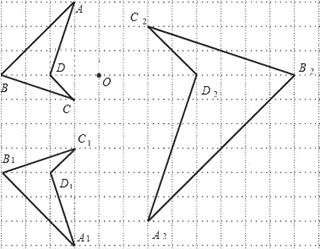
(1)图形ABCD与图形A1B1C1D1关于直线MN成轴对称,请在图中画出对称轴并标注上相应字母M、N;
(2)以图中O点为位似中心,将图形ABCD放大,得到放大后的图形A2B2C2D2,则图形ABCD与图形A2B2C2D2的对应边的比是多少(注:只要写出对应边的比即可);
(3)求图形A2B2C2D2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
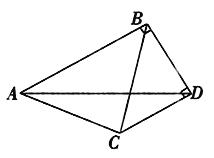
【题目】如图,△ABD和△BDC都是直角三角形,且∠ABD=∠BDC=90°,∠BAD=30°,∠DBC=45°,则tan∠DAC的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列函数:(1)y=3﹣2x2;(2)y=![]() ;(3)y=3x(2x﹣1);(4)y=﹣2
;(3)y=3x(2x﹣1);(4)y=﹣2![]() x2;(5)y=x2﹣(3+x)2;(6)y=mx2+nx+p(其中m、n、p为常数).其中一定是二次函数的有( )
x2;(5)y=x2﹣(3+x)2;(6)y=mx2+nx+p(其中m、n、p为常数).其中一定是二次函数的有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
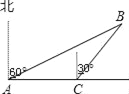
【题目】某民航飞机在大连海域失事,为调查失事原因,决定派海军潜水员打捞飞机上的黑匣子,如图所示,一潜水员在A处以每小时8海里的速度向正东方向划行,在A处测得黑匣子B在北偏东60°的方向,划行半小时后到达C处,测得黑匣子B在北偏东30°的方向,在潜水员继续向东划行多少小时,距离黑匣子B最近,并求最近距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com