练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

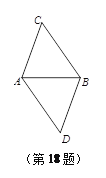
    【题目】如图，将线段AB绕点A逆时针旋转α度角得到线段AC，将线段AB绕点B逆时针旋转α度角得到线段BD（0°<α<180°），连结BC、AD．当α=_______度时，四边形ACBD是菱形，并说明理由．

    【答案】60

    【解析】分析：根据旋转的性质得到AC=AB，∠CAB=60°．判定△ABC为等边三角形．

    进一步判定四边形ACBD是平行四边形．根据AC=BC，即可判定四边形ACBD是菱形.

    详解：60

    理由如下：

    ∵线段AB绕点A逆时针旋转60°得到线段AC，

    ∴AC=AB，∠CAB=60°．

    ∴△ABC为等边三角形．

    ∴AC=BC．

    ∵线段AB绕点B逆时针旋转60°得到线段BD，

    ∴BD=AB，∠ABD=60°．

    ∴AC=BD，∠CAB=∠ABD．

    ∴AC∥BD．

    ∴四边形ACBD是平行四边形．

    ∵AC=BC，

    ∴四边形ACBD是菱形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

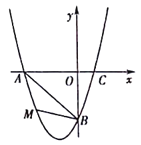
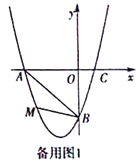
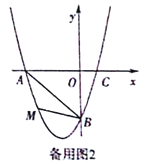
    【题目】在平面直角坐标系中，已知抛物线经过A(－3，0)，B(0，－3)，C(1，0)三点.

    (1)求抛物线的解析式；

    (2)若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S.求S

    关于m的函数关系式，并求出S的最大值；

    (3)若点P是抛物线上的动点，点Q是直线y=－x上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2017年5月14日至15日，“一带一路”国际合作高峰论坛在北京举行，本届论坛期间，中国同30多个国家签署经贸合作协议，某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区，已知2件甲种商品与3件乙种商品的销售收入相同，3件甲种商品比2件乙种商品的销售收入多1500元.

    (1)甲种商品与乙种商品的销售单价各多少元？

    (2)若甲、乙两种商品的销售总收入不低于5400万元，则至少销售甲种商品多少万件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①abc＞0；②4ac﹣b2＜0；③4a+c＜2b；④3b+2c＜0；⑤m（am+b）+b＜a（m≠﹣1）．其中结论正确的个数是（　　）

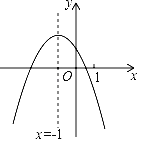
    A. 2 B. 3 C. 4 D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与坐标轴交于点、两点，直线与直线相交于点，交轴于点，且的面积为.

    (1)求的值和点的坐标；

    (2)求直线的解析式；

    (3)若点是线段上一动点，过点作轴交直线于点，轴，轴，垂足分别为点、，是否存在点，使得四边形为正方形，若存在，请求出点坐标，若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）正方形ABCD，E、F分别在边BC、CD上（不与端点重合），∠EAF＝45°，EF与AC交于点G

    ①如图（i），若AC平分∠EAF，直接写出线段EF，BE，DF之间等量关系；

    ②如图（ⅱ），若AC不平分∠EAF，①中线段EF，BE，DF之间等量关系还成立吗？若成立请证明；若不成立请说明理由

    （2）如图（ⅲ），矩形ABCD，AB＝4，AD＝8．点M、N分别在边CD、BC上，AN＝2，∠MAN＝45°，求AM的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．

    （1）探究：线段OE与OF的数量关系并加以证明；

    （2）当点O在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明；若不是，则说明理由；

    （3）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将下列各数填到相应的集合里：

    -，+5，-9，π，，19, 1.2, 0，-5.26,0.8256…，5.3

    正数集合﹛ …﹜

    负数集合﹛ …﹜

    整数集合﹛ …﹜

    分数集合﹛ …﹜

    有理数集合﹛ …﹜

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，C地位于A、B两地之间，甲步行直接从C地前往B地，乙骑自行车由C地先回A地，再从A地前往B地（在A地停留时间忽略不计），已知两人同时出发且速度不变，乙的速度是甲的2.5倍，设出发xmin后，甲、乙两人离C地的距离为y1m、y2m，图②中线段OM表示y1与x的函数图象．

    （1）甲的速度为______m/min．乙的速度为______m/min．

    （2）在图②中画出y2与x的函数图象，并求出乙从A地前往B地时y2与x的函数关系式．

    （3）求出甲、乙两人相遇的时间．

    （4）请你重新设计题干中乙骑车的条件，使甲、乙两人恰好同时到达B地．

    要求：①不改变甲的任何条件．

    ②乙的骑行路线仍然为从C地到A地再到B地．

    ③简要说明理由．

    ④写出一种方案即可．

    查看答案和解析>>

    同步练习册答案