
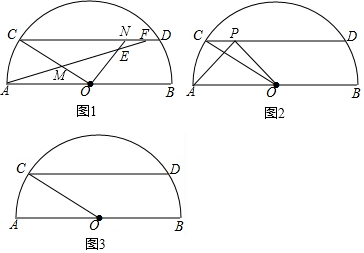
分析 (1)①作出两圆的外公切线,利用弦切角和圆周角的关系即可得出∠AED=∠ACB,即可;
②先判断出AM平分∠BAC,AN⊥DE,进而得出∠DAN=30°,再求出∠DOI=60°,进而用含30°的直角三角形的性质判断出AD=ND,即可求出∠AND=30°,进而判断出∠DON+∠DNO=90°,即可得出结论.
③先判断出AN⊥BC,进而求出MN=BN=$\sqrt{2}$a,再用勾股定理得出AM=BM=2a,进而用勾股定理求出AB的平方,最后判断出AD=$\frac{1}{2}$AB代入即可;
(2)作出辅助线,先判断出四边形ADME的面积等于四边形AHMGA的面积,进而转化成三角形AMH的面积的2倍,再判断出HM=$\frac{1}{2}$AH,用面积公式求的AH=3,最后判断出AB=2AH即可得出结论.
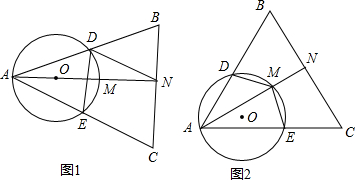
解答 解:(1)①如图1,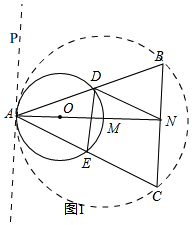
∵线段AM为⊙O的直径,
∴⊙O,⊙M内切于点A,
过点A作⊙O,⊙M的外公切线PA,
在⊙O中,∠PAD=∠AED,
在⊙M中,∠PAD=∠ACB,
∴∠AED=∠ACB,
∴DE∥BC,
②如图1-1,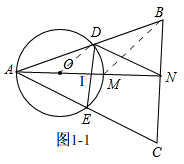
∵AM是⊙O的直径,且AD=AE,
∴AM平分∠BAC,AN⊥DE,
∴∠DAN=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×60°=30°,
连接OD,∴OA=OD,
∴∠OAD=∠ODA=30°,
在Rt△ODI中,∠DOI=2∠OAD=60°,
∴∠ODI=30°,
∴DI=$\sqrt{3}$OI,OA=OD=2OI,
∴AM=2OA=4OI,AI=OA+OI=3OI,
∴IM=AM-AI=4OI-3OI=OI,
∵M是△ABC的外心,
∴BM=AM=4OI,∠BMN=2∠BAN=60°,
∴∠MBN=30°,
在Rt△BMN中,MN=$\frac{1}{2}$BM=2OI,
∴NI=IM+MN=OI+2OI=3OI,
∴AI=NI,
∵DE⊥AN,
∴AD=DN,
∴∠DNI=∠DAI=30°,
∴∠NDI=60°,
∴∠ODN=∠ODI+∠NDI=90°,
∵D在⊙O上,
∴直线DN是⊙O的切线;
③如图2,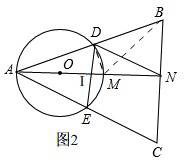 连接DM,BM,
连接DM,BM,
∵AM是⊙O的直径,且AD=AE,
∴AM平分∠BAC,AN⊥DE,
∴BN=$\frac{1}{2}$BC=$\sqrt{2}$a,∠DAN=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×45°=22.5°,
∴∠ABN=90°-∠DAN=67.5°,
∵M是△ABC的外心,
∴∠BMN=2∠BAN=45°,
在Rt△BMN中,MN=BN=$\sqrt{2}$a,BM=$\sqrt{2}$BN=2a,
∴AM=BM=2a,
∴AN=AM+MN=2a+$\sqrt{2}$a=(2+$\sqrt{2}$)a,
在Rt△ABN中,AB2=AN2+BN2=[(2+$\sqrt{2}$)a]2+2a2=(8+4$\sqrt{2}$)a2,
连接DM,
∵AM是⊙O的直径,
∴∠ADM=90°,
∵AM=BM,
∴AD=$\frac{1}{2}$AB,
∴AD2=($\frac{1}{2}$AB)2=$\frac{1}{4}$AB2=$\frac{1}{4}$(8+4$\sqrt{2}$)a2=(2+$\sqrt{2}$)a2.
(2)∵点M是等边三角形ABC的外心,
∴AM=BM,AN⊥BC,AN平分∠BAC,
过点M作MH⊥AB,MG⊥AC,
∴MH=MG,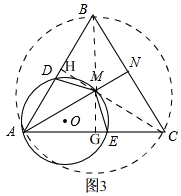
∵四边形ADME是⊙O的内接圆,
∴∠HDM=∠GEM,
在△DHM和△EGM中,$\left\{\begin{array}{l}{∠HDM=∠GEM}\\{∠DHM=∠EGM}\\{MH=MG}\end{array}\right.$,
∴△DHM≌△EGM,
∴S△DHM=S△EGM,
∴S四边形ADME=S四边形AHMG=2S△AHM=2×$\frac{1}{2}$AH×HM=AH×HM=3$\sqrt{3}$,
∵AN平分∠BAC,
∴∠BAN=$\frac{1}{2}$∠BAC=30°,
∴HM=$\frac{\sqrt{3}}{3}$AH,
∴AH×$\frac{\sqrt{3}}{3}$AH=3$\sqrt{3}$,
∴AH=3,
∵AM=BM,MH⊥AB,
∴AB=2AH=6.
点评 此题圆的综合题,主要考查了三角形的外接圆的性质,等边三角形的性质,含30°角的直角三角形的性质,圆内接四边形的性质,角平分线的性质,全等三角形的判定和性质,勾股定理,切线的判定,解本题的关键是判断出AN垂直平分BC.


科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:填空题
定义一种新运算“※”,规定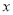 ※
※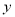 =
= 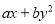 ,其中
,其中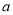 、
、 为常数,且1※2=5,2※1=6, 则2※3=____________ 。
为常数,且1※2=5,2※1=6, 则2※3=____________ 。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y2<0<y1 | B. | y1<0<y2 | C. | y1<y2<0 | D. | y2<y1<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 铁路上A,B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,请画出E点位置(要求尺规作图,保留作图痕迹)并求出E站应建在离A站多少千米处?
铁路上A,B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,请画出E点位置(要求尺规作图,保留作图痕迹)并求出E站应建在离A站多少千米处?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com