
【题目】某篮球队在一次联赛中共进行了10场比赛,已知这10场比赛的平均得分为48分,且前9场比赛的得分依次为:57,51,45,51,44,46,45,42,48.
(1)求第10场比赛的得分;
(2)直接写出这10场比赛的中位数,众数和方差.
方差公式:s2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2]
)2]
【答案】(1)51(2)18.2
【解析】
(1)根据平均数的定义先求出总数,再分别减去前9个数即可;
(2)根据中位数、众数的定义分别求出最中间两个数的平均数和出现次数最多数,再根据方差的计算公式代入计算即可.
(1)∵10场比赛的平均得分为48分,
∴第10场比赛的得分=48×10﹣57﹣51﹣45﹣51﹣44﹣46﹣45﹣42﹣48=51(分),
(2)把这10个数从小到大排列为;42、44、45、45、46、48、51、51、51、57,
最中间两个数的平均数是(46+48)÷2=47,
则这10场比赛得分的中位数为47分,
∵51都出现了最多次数3次,所以众数为51,
方差=![]() [(42﹣48)2+(44﹣48)2+2×(45﹣48)2+(46﹣48)2+(48﹣48)2+3×(51﹣48)2+(57﹣48)2]=18.2.
[(42﹣48)2+(44﹣48)2+2×(45﹣48)2+(46﹣48)2+(48﹣48)2+3×(51﹣48)2+(57﹣48)2]=18.2.
故答案为:(1)51(2)18.2.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何体的三视图相互关联.已知直三棱柱的三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=![]() .
.
(1)求BC及FG的长;
(2)若主视图与左视图两矩形相似,求AB的长;
(3)在(2)的情况下,求直三棱柱的表面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
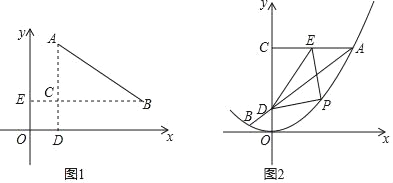
【题目】(1)如图1,若点A坐标为(x1,y1),点B坐标为(x2,y2),作AD⊥x轴于点D,BE⊥y轴于点E,AD与BE相交于点C,则有AC=|y1﹣y2|,BC=|x1﹣x2|,所以,A、B两点间的距离为AB=![]() .
.
根据结论,若M、N两点坐标分别为(1,4)、(5,1),则MN= (直接写出结果).
(2)如图2,直线y=kx+1与y轴相交于点D,与抛物线y=![]() x2相交于A,B两点,A点坐标为(4,a),过点A作y轴的垂线交y轴于点C,E是AC中点,点P是第一象限内直线AB下方抛物线上一动点,连接PE、PD、ED;
x2相交于A,B两点,A点坐标为(4,a),过点A作y轴的垂线交y轴于点C,E是AC中点,点P是第一象限内直线AB下方抛物线上一动点,连接PE、PD、ED;
①a= ,k= ,AD= (直接写出结果).
②若△DEP是以DE为底的等腰三角形,求点P的横坐标;
③求四边形CDPE的周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
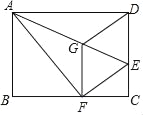
【题目】如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
①∠ADG=∠AFG;②四边形DEFG是菱形;③DG2=![]() AEEG;④若AB=4,AD=5,则CE=1.
AEEG;④若AB=4,AD=5,则CE=1.
A. ①②③④ B. ①②③ C. ①③④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
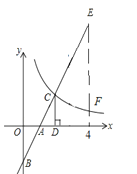
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A,B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②![]() ;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,则巡逻船从出发到成功拦截捕鱼船所用的时间是( )

A. 1小时 B. 2小时 C. 3小时 D. 4小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com