
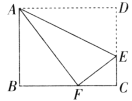
【题目】如图,折叠矩形纸片的一边AD,使点D落在BC边上的点F处,BC=10cm, AB=8cm, 则EC的长为_________.
【答案】3cm
【解析】由矩形的性质可得CD=AB=8,AD=BC=10,由折叠的性质可得AF=AD=10,DE=EF,∠AFE=∠D=90°,在Rt△ABF中,由勾股定理可求出BF的长,继而可得FC的长,设CE=x,则DE=8-x,EF= DE=8-x,在Rt△CEF中,利用勾股定理即可救出CE的长.
∵四边形ABCD为矩形,
∴CD=AB=8,AD=BC=10,
∵折叠矩形ABCD的一边AD,使点D落在BC边的点F处,
∴AF=AD=10,DE=EF,∠AFE=∠D=90°,
在Rt△ABF中,BF=![]() =6,
=6,
∴FC=BC-BF=4,
设CE=x,则DE=8-x,EF= DE=8-x,
在Rt△CEF中,
∵CF2+CE2=EF2,
∴42+x2=(8-x)2,解得x=3,
即CE=3cm,
故答案为:3cm.


科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其坡度为i=1: ![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比) 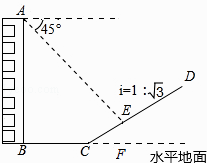
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票零售价为80元/张,“五一”黄金周期间,甲乙两家旅行社推出优惠活动,甲旅行社一律九折优惠;乙旅行社对10人以内(含10人)不优惠,超过10人超出部分八折优惠,某班部分同学去该景点旅游.设参加旅游人数为x人,购买门票需要y元.
(1)分别直接写出两家旅行社y与x的函数关系式,并写出对应自变量x的取值范围;
(2)请根据该班旅游人数设计最省钱的购票方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运40千克,A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等.设B型机器人每小时搬运化工原料x千克,根据题意可列方程为( )
A.![]() =
= ![]()
B.![]() =
= ![]()
C.![]() =
= ![]()
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
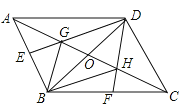
【题目】如图,已知G、H是△ABC的边AC的三等分点,GE∥BH,交AB于点E,HF∥BG交BC于点F,延长EG、FH交于点D,连接AD、DC,设AC和BD交于点O,求证:四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把对角线互相垂直的四边形叫做垂美四边形.
(1)(概念理解)在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是___________.
(2)(性质探究)如图2,试探索垂美四边形ABCD的两组对边AB,CD与BC ,AD之间的数量关系,写出证明过程。
(3)(问题解决)如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外做正方形ACFG和正方形ABDE,连接CE,BG,GE, 已知AC=![]() ,BC=1 求GE的长.
,BC=1 求GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在同一次测试中,从两校各随机抽取了30名学生的测试成绩进行调查分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分.
甲校 93 82 76 77 76 89 89 89 83 87 88 89 84 92 87
89 79 54 88 92 90 87 68 76 94 84 76 69 83 92
乙校 84 63 90 89 71 92 87 92 85 61 79 91 84 92 92
73 76 92 84 57 87 89 88 94 83 85 80 94 72 90
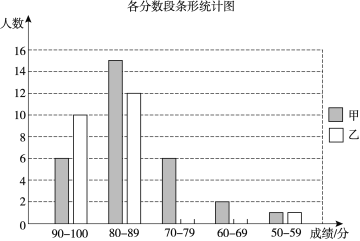
(1)请根据乙校的数据补全条形统计图;
(2)两组样本数据的平均数、中位数、众数如下表所示,请补全表格;
平均数 | 中位数 | 众数 | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
(3)两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些,
请为他们各写出一条可以使用的理由;
甲校: .乙校: .
(4)综合来看,可以推断出 校学生的数学学业水平更好一些,理由为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人5次射击命中的环数如下:
甲 | 7 | 9 | 8 | 6 | 10 |
乙 | 7 | 8 | 9 | 8 | 8 |
则以下判断中正确的是( )
A.![]() 甲=
甲= ![]() 乙 , S甲2=S乙2 .
乙 , S甲2=S乙2 .
B.![]() 甲=
甲= ![]() 乙 , S甲2>S乙2 .
乙 , S甲2>S乙2 .
C.![]() 甲=
甲= ![]() 乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 .
D.![]() 甲<
甲< ![]() 乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:德国著名数学家高斯被认为是历史上最重要的数学家之一,并有"数学王子"的美誉.高斯从小就善于观察和思考.在他读小学时候就能在课堂上快速的计算出![]() ,今天我们可以将高斯的做法归纳如下:
,今天我们可以将高斯的做法归纳如下:
令![]() ①
①
![]() ②
②
(右边相加100+1=2+99=3+98=…..=100+1共100组)
①+②:有2S=101x100 解得:![]()
(1)请参照以上做法,回答,3+5+7+9+…..+97= ;
请尝试解决下列问题:
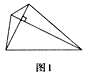
如下图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.

(2)填写下表:
层数 | 1 | 2 | 3 | 4 |
该层对应的点数 | 1 | 6 | 12 | 18 |
所有层的总点数的和 | 1 | 7 | 19 |
①写出第n层所对应的点数;(n≥2)
②如果某一层共96个点,求它是第几层;
③写出n层的六边形点阵的总点数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com