
分析 (1)原式利用幂的乘方与积的乘方运算法则计算,合并即可得到结果;
(2)原式变形后,利用同底数幂的乘法法则计算,合并即可得到结果;
(3)原式第一项利用零指数幂法则计算,第二项利用负整数指数幂法则计算,第三项利用乘方的意义化简,最后一项利用负整数指数幂法则计算即可得到结果;
(4)原式第二项利用负整数指数幂法则计算,第三项利用绝对值的代数意义化简,最后一项利用零指数幂法则计算即可得到结果.
解答 解:(1)原式=-x5+2x5+x5=2x5;
(2)原式=(a-b)6-(a-b)6=0;
(3)原式=1-$\frac{1}{8}$+9-4=$\frac{47}{8}$;
(4)原式=5-3+3-1=4.
点评 此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 随机抛一枚硬币,落地后正面一定朝上 | |
| B. | 调查重庆市民对诺贝尔文学奖获得者莫言的知晓情况用普查 | |
| C. | 在一副没有大小王的扑克牌中任意抽一张,抽到的牌是6的概率是$\frac{1}{13}$ | |
| D. | 在一次抽奖活动中,”中奖率是$\frac{1}{100}$”表示抽奖100次就一定会中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
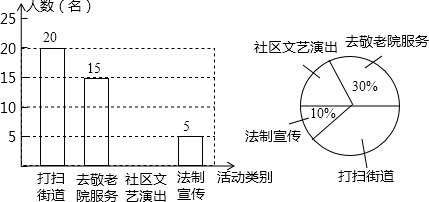
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com