
分析 首先根据条件x2+y2=6xy进行配方可得(x+y)2=8xy,(x-y)2=4xy,进而可得x+y=$\sqrt{8xy}$,x-y=$\sqrt{4xy}$,然后再代入求值即可.
解答 解:∵x2+y2=6xy,
∴x2+2xy+y2=8xy,x2-2xy+y2=4xy,
∴(x+y)2=8xy,(x-y)2=4xy,
∵x>y>0,
∴x+y=$\sqrt{8xy}$,x-y=$\sqrt{4xy}$,
∴$\frac{x-y}{x+y}$=$\frac{\sqrt{4xy}}{\sqrt{8xy}}$=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 此题主要考查了分式的值,在解答时应从已知条件和所求问题的特点出发,通过适当的变形、转化,才能发现解题的捷径.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,CB、CD分别是钝角三角形AEC和锐角三角形ABC的中线,且∠ACB=∠ABC,AB=AC,给出下列结论:①AE=2AC;②CE=2CD;③∠ACD=∠BCE;④CB是∠DCE的平分线.正确的结论序号是( )
如图,CB、CD分别是钝角三角形AEC和锐角三角形ABC的中线,且∠ACB=∠ABC,AB=AC,给出下列结论:①AE=2AC;②CE=2CD;③∠ACD=∠BCE;④CB是∠DCE的平分线.正确的结论序号是( )| A. | ①②③ | B. | ①②④ | C. | ①②③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{m}=\frac{n}{b}$ | B. | $\frac{a}{n}=\frac{m}{b}$ | C. | $\frac{m}{a}=\frac{n}{b}$ | D. | $\frac{m}{a}=\frac{b}{n}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
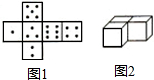 有同样大小的三个立方体骰子,每个骰子的展开图如图1所示,如果把每个骰子点数是4的一面放在桌子上,那么其它五个可以看到的面上的数字的和是17,现在把三个骰子放在桌子上(如图2),凡是能看得到的点数之和最大是51,最小是26.
有同样大小的三个立方体骰子,每个骰子的展开图如图1所示,如果把每个骰子点数是4的一面放在桌子上,那么其它五个可以看到的面上的数字的和是17,现在把三个骰子放在桌子上(如图2),凡是能看得到的点数之和最大是51,最小是26.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com