
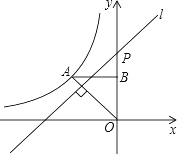
【题目】如图,反比例函数y=![]() (x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.
(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.
【答案】1+![]()
【解析】根据反比例函数图象上点的坐标特征由A点坐标为(-2,2)得到k=-4,即反比例函数解析式为y=-![]() ,且OB=AB=2,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后由轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则点B′的坐标可表示为(-
,且OB=AB=2,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后由轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则点B′的坐标可表示为(-![]() ,t),于是利用PB=PB′得t-2=|-
,t),于是利用PB=PB′得t-2=|-![]() |=
|=![]() ,然后解方程可得到满足条件的t的值.
,然后解方程可得到满足条件的t的值.
∵点A坐标为(-2,2),
∴k=-2×2=-4,
∴反比例函数解析式为y=-![]() ,
,
∵OB=AB=2,
∴△OAB为等腰直角三角形,
∴∠AOB=45°,
∵PQ⊥OA,
∴∠OPQ=45°,
∵点B和点B′关于直线l对称,
∴PB=PB′,BB′⊥PQ,
∴∠B′PQ=∠OPQ=45°,∠B′PB=90°,
∴B′P⊥y轴,
∴点B′的坐标为(-![]() ,t),
,t),
∵PB=PB′,
∴t-2=|-![]() |=
|=![]() ,
,
整理得t2-2t-4=0,解得t1=1+![]() ,t2=1-
,t2=1-![]() (不符合题意,舍去),
(不符合题意,舍去),
∴t的值为1+![]() ,
,
故答案为:1+![]() .
.



科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;
(1)如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数;
(2)如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由.
(3)如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )

A. ∠1=∠3 B. ∠B+∠BCD=180°
C. ∠2=∠4 D. ∠D+∠BAD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
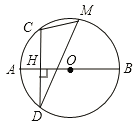
【题目】如图,线段AB 是⊙O的直径,弦CD⊥AB于点H,点M是弧CBD 上任意一点,AH=2,CH=4.
(1)求⊙O 的半径r 的长度;
(2)求sin∠CMD;
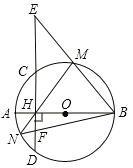
(3)直线BM交直线CD于点E,直线MH交⊙O 于点 N,连接BN交CE于点 F,求HE![]() HF的值.
HF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8,AC=6.点D在边AB上,AD=4.5.△ABC的角平分线AE交CD于点F.
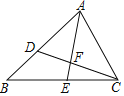
(1)求证:△ACD∽△ABC;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点 O 是直线 AB上一点,∠COD 是直角,OE平分∠BOC.
(1)①如图1,若∠DOE=25°,求∠AOC 的度数;
②如图2,若∠DOE=α,直接写出∠AOC的度数(用含α的式子表示);
(2)将图 1中的∠COD 绕点O按顺时针方向旋转至图 2 所示位置.探究∠DOE 与∠AOC 的度数之间的关系,写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
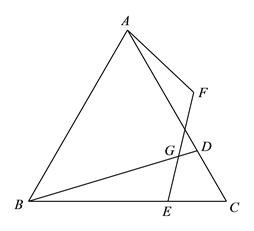
【题目】如图,在等边![]() 中,
中, ![]() 分别是边
分别是边![]() 上的点,且
上的点,且![]() ,
,![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,
,![]() 交
交![]() 于
于![]() .
.
(1)连接![]() ,则
,则![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)若![]() ,求
,求![]() 的大小(用
的大小(用![]() 的式子表示)
的式子表示)
(2)用等式表示线段![]() 和
和![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
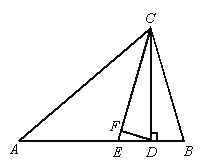
【题目】如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,
(1)试说明CD是△CBE的角平分线;
(2)和∠B相等的角是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江中下游地区特大旱情发生后,全国人民抗旱救灾,众志成城.市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,温州市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com