
【题目】某地区果农收获草莓30吨,枇杷13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往省城,已知甲种货车可装草莓4吨和枇杷1吨,乙种货车可装草莓、枇杷各2吨.
(1)该果农安排甲、乙两种货车时有几种方案请您帮助设计出来;
(2)若甲种货车每辆要付运输费2 000元,乙种货车每辆要付运输费1 300元,则该果农应选择哪种运输方案才能使运费最少,最少运费是多少元?
【答案】(1)方案一:安排甲种货车5辆,乙种货车5辆;方案二:安排甲种货车6辆,乙种货车4辆;(2)选择方案一,甲.乙两种货车各安排5辆运输这批水果时,总运费最少,最少运费是16 500元
【解析】
试题(1)先设甲种货车为x辆,则乙种货车为(10-x)辆,列出一元一次不等式组,再进行计算,即可求出答案.
(2)根据甲货车的费用和乙货车的费用得出费用最少的方案,再进行计算即可.
(1)设李大叔安排甲货车x辆,则乙货车为(10-x)辆,据题意得:
![]() ,
,
解得5≤x≤7,
∵x应是整数,
∴x=5或x=6或x=7
∴有三种运输方案:方案一,安排5辆甲货车,5辆乙货车
方案二,安排6辆甲货车,4辆乙货车;
方案三,安排7辆甲货车,3辆乙货车;
(2)∵甲货车的运费大于乙货车运费,所以选方案一的费用最少.
∴其运费为2000×5+1300×5=16500(元).
答:李大叔应选方案一,才能使运费最少,最少运费是16500元.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
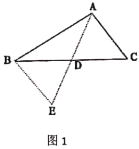
【题目】课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将
的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,把
,把![]() 、
、![]() 、
、![]() 集中在
集中在![]() 中,利用三角形的三边关系可得
中,利用三角形的三边关系可得![]() ,则
,则![]() ;
;
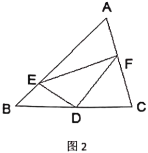
(2)问题解决:受到(1)的启发,请你证明下面命题:如图2,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
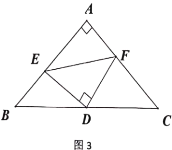
②如图3,若![]() ,探索线段
,探索线段![]() 、
、![]() 、
、![]() 之间的等量关系,并加以证明.
之间的等量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
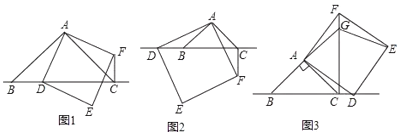
【题目】类比思想就是根据已经学习过的知识,类比探究新知识的思想方法.我们在探究矩形、菱形、正方形等问题中的数量关系时,经常用到类比思想.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在![]() 中,
中,![]() 点
点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 重合),以
重合),以![]() 为边在
为边在![]() 右侧作正方形
右侧作正方形![]() 连接
连接![]() .
.
(1)(观察猜想)如图①,当点![]() 在线段
在线段![]() 上时;
上时;
①![]() 与
与![]() 的位置关系为: ;
的位置关系为: ;
②![]() 之间的数量关系为: ;(将结论直接写在横线上)
之间的数量关系为: ;(将结论直接写在横线上)
(2)(数学思考)如图②,当点![]() 在线段
在线段![]() 的延长线上时,结论①②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
的延长线上时,结论①②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(3)(拓展延伸)如图③,当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若已知
.若已知![]() 请直接写出
请直接写出![]() 的长.(提示: .过
的长.(提示: .过![]() 作
作![]() 于
于![]() 过
过![]() 作
作![]() 于
于![]() 于
于![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=36°,OE平分∠MON,点A,B分别是射线OM,OE,上的动点(A,B不与点O重合),点D是线段OB上的动点,连接AD并延长交射线ON于点C,设∠OAC=x,
(1)如图1,若AB∥ON,则
①∠ABO的度数是______;
②当∠BAD=∠ABD时,x=______;
当∠BAD=∠BDA时,x=______;
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ABD中有两个相等的角?若存在,求出x的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB、AD是⊙O的弦,点C是DO的延长线与弦AB的交点,∠ABO=30°,OB=2.
(1)求弦AB的长;
(2)若∠D=20°,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,地面上小山的两侧有A,B两地,为了测量A,B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟40m的速度直线飞行,10分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.(结果用含非特殊角的三角函数和根式表示即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月31日,2019长安汽车重庆国际马拉松赛在南滨路鸣枪开跑,小育和小才参加了此次比赛,小育在跑出![]() 小时后不慎摔倒,志愿者将小育扶到路旁处理伤口,休息了
小时后不慎摔倒,志愿者将小育扶到路旁处理伤口,休息了![]() 分钟后决定再次出发,在小育出发
分钟后决定再次出发,在小育出发![]() 小时后小才追上小育,如图所示是两人离开出发地的距离
小时后小才追上小育,如图所示是两人离开出发地的距离![]() (公里)和出发时间
(公里)和出发时间![]() (小时)之间的函数图象.当小才到达终点时,小育距离终点____公里.
(小时)之间的函数图象.当小才到达终点时,小育距离终点____公里.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,对角线
中,对角线![]() ,
,![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
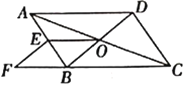
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当线段![]() 和
和![]() 之间满足什么条件时,四边形
之间满足什么条件时,四边形![]() 是矩形?并说明理由;
是矩形?并说明理由;
(3)当线段![]() 和
和![]() 之间满足什么条件时,四边形
之间满足什么条件时,四边形![]() 是正方形?并说明理由.
是正方形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com