练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD为平行四边形，F是CD的中点，连接AF并延长与BC的延长线交于点E．求证：BC=CE．

    【答案】证明：如图，∵四边形ABCD是平行四边形， ∴AD=BC，AD∥BC，
    ∴∠DAF=∠E，∠ADF=∠ECF，
    又∵F是CD的中点，即DF=CF，
    ∴△ADF≌△ECF，
    ∴AD=CE，
    ∴BC=CE．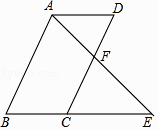

    【解析】根据平行四边形的对边平行且相等可得AD=BC，AD∥BC，根据两直线平行，内错角相等可得∠DAF=∠E，∠ADF=∠ECF，根据线段中点的定义可得DF=CF，然后利用“角角边”证明△ADF≌△ECF，根据全等三角形对应边相等可得AD=CE，从而得证．
    【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

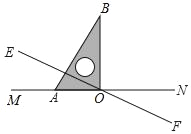
    【题目】如图，直线EF与MN相交于点O，∠MOE=30°，将一直角三角尺的直角顶点与点O重合，直角边OA与MN重合，OB在∠NOE内部．操作：将三角尺绕点O以每秒5°的速度沿顺时针方向旋转一周，设运动时间为t（s）．

    (1)当t为何值时，直角边OB恰好平分∠NOE？此时OA是否平分∠MOE？请说明理由；

    (2)若在三角尺转动的同时，直线EF也绕点O以每秒8°的速度顺时针方向旋转一周，当一方先完成旋转一周时，另一方同时停止转动．

    ①当t为何值时，OE平分∠AOB？

    ②OE能否平分∠NOB？若能请直接写出t的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，有四张背面完全相同的纸牌A、B、C、D，其正面分别画有四个不同的几何图形，将这四张纸牌背面朝上洗匀．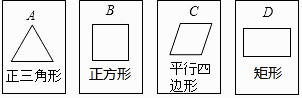

    （1）从中随机摸出一张，求摸出的牌面图形是中心对称图形的概率；
    （2）小明和小亮约定做一个游戏，其规则为：先由小明随机摸出一张纸牌，不放回，再由小亮从剩下的纸牌中随机摸出一张，若摸出的两张牌面图形都是轴对称图形小明获胜，否则小亮获胜，这个游戏公平吗？请用列表法（或树状图）说明理由（纸牌用A、B、C、D表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    （1）计算：（﹣1）3÷（﹣5）2×（﹣）﹣|0.8﹣1|；

    （2）计算：（1+﹣2.75）×（﹣24）+（﹣1）2011﹣|﹣2|；

    （3）先化简，再求值，已知|x+2|+（y﹣）2=0，求3（x2﹣2xy）﹣[3x2﹣2y+2（xy+y）]的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

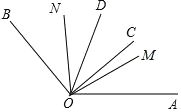
    【题目】①下午 2 点 10 分时，钟表的时针和分针所成锐角是________；

    ②如图，射线 OC，OD 在∠AOB 的内部，射线 OM，ON 分别平分∠AOD，∠BOC， 且∠BON=50°，∠AOM=40°，∠COD=30°，则∠AOB 的度数为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一副三角板中的两块直角三角尺的直角顶点 O 按如图方式叠放在一起．

    （ 1 ） 如图 1 ， 若∠ BOD=35° ， 则∠ AOC= ； 若∠AOC=135°， 则∠BOD= ；

    （2）如图2，若∠AOC=140°，则∠BOD= ；

    （3）猜想∠AOC 与∠BOD 的大小关系，并结合图1说明理由．

    （4）三角尺 AOB 不动，将三角尺 COD 的 OD 边与 OA 边重合，然后绕点 O 按顺时针或逆时针方向任意转动一个角度，当∠A OD（0°＜∠AOD＜90°）等于多少度时，这两块三角尺各有一条边互相垂直，直接写出∠AOD 角度所有可能的值，不用说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    (1)5﹣（﹣3）+（﹣2）﹣1；

    (2)2×（﹣）÷（﹣3）；

    (3)﹣5×[1﹣（0.5+ ）÷]；

    (4)20×（﹣）+4×（﹣）+2×（﹣）；

    (5)﹣14-（）÷（﹣）×[﹣2﹣（﹣3）2]﹣(﹣0.52)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线的解析表达式为：y=－3x＋3，且与x轴交于点D，直线经过点A，B，直线，交于点C．

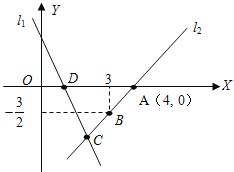
    （1）求点D的坐标；

    （2）求直线的解析表达式；

    （3）求△ADC的面积；

    （4）在直线上存在异于点C的另一点P，使得△ADP的面积是△ADC面积的2倍，请直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在现实生活中，我们会看到许多“标准”的矩形，如我们的课本封面、A4的打印纸等，其实这些矩形的长与宽之比都为 ：1，我们不妨就把这样的矩形称为“标准矩形”，在“标准矩形”ABCD中，P为DC边上一定点，且CP=BC，如图所示．
    （1）如图①，求证：BA=BP；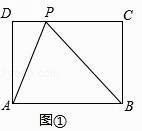

    （2）如图②，点Q在DC上，且DQ=CP，若G为BC边上一动点，当△AGQ的周长最小时，求 的值；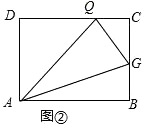

    （3）如图③，已知AD=1，在（2）的条件下，连接AG并延长交DC的延长线于点F，连接BF，T为BF的中点，M、N分别为线段PF与AB上的动点，且始终保持PM=BN，请证明：△MNT的面积S为定值，并求出这个定值．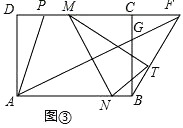

    查看答案和解析>>

    同步练习册答案