
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:
,下列结论: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 若点
若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
; ![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() 其中正确的结论是______.
其中正确的结论是______.
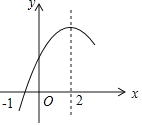
【答案】(1)(3)(5)
【解析】分析:(1)正确.根据对称轴公式计算即可.
(2)错误,利用x=-3时,y<0,即可判断.
(3)正确.由图象可知抛物线经过(-1,0)和(5,0),列出方程组求出a、b即可判断.
(4)错误.利用函数图象即可判断.
(5)正确.利用二次函数与二次不等式关系即可解决问题.
详解:(1)正确.∵-![]() =2,
=2,
∴4a+b=0.故正确.
(2)错误.∵x=-3时,y<0,
∴9a-3b+c<0,
∴9a+c<3b,故(2)错误.
(3)正确.由图象可知抛物线经过(-1,0)和(5,0),
∴![]()
解得![]() ,
,
∴8a+7b+2c=8a-28a-10a=-30a,
∵a<0,
∴8a+7b+2c>0,故(3)正确.
(4)错误,∵点A(-3,y1)、点B(-![]() ,y2)、点C(
,y2)、点C(![]() ,y3),
,y3),
∵![]() -2=
-2=![]() ,2-(-
,2-(-![]() )=
)=![]() ,
,
∴![]() <
<![]()
∴点C离对称轴的距离近,
∴y3>y2,
∵a<0,-3<-![]() <2,
<2,
∴y1<y2
∴y1<y2<y3,故(4)错误.
(5)正确.∵a<0,
∴(x+1)(x-5)=-3/a>0,
即(x+1)(x-5)>0,
故x<-1或x>5,故(5)正确.
∴正确的有三个,
故正确的是(1)(3)(5).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】网店店主小李进了一批某种商品,每件进价10元.预售一段时间后发现:每天销售量![]() (件)与售价
(件)与售价![]() (元/件)之间成一次函数关系:
(元/件)之间成一次函数关系:![]() .
.
(1)小李想每天赚取利润150元,又要使所进的货尽快脱手,则售价定为多少合适?
(2)小李想每天赚取利润300元,这个想法能实现吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要得到DG∥BC,则需要条件( )
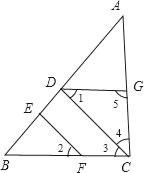
A. CD⊥AB,EF⊥AB B. ∠1=∠2
C. ∠1=∠2,∠4+∠5=180° D. CD⊥AB,EF⊥AB,∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
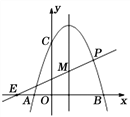
【题目】如图,已知抛物线![]()
![]() 与
与![]() 轴交于A(-1,0),B(3,0)两点,与
轴交于A(-1,0),B(3,0)两点,与![]() 轴交于点C(0,3),动点P在抛物线上,直线PE与抛物线的对称轴交于点M,点E的坐标为(-2,0).
轴交于点C(0,3),动点P在抛物线上,直线PE与抛物线的对称轴交于点M,点E的坐标为(-2,0).
(1)求抛物线的函数表达式;
(2)若P与C关于抛物线的对称轴对称,求直线PE的函数表达式;
(3)若PM=![]() EM,求点P的坐标.
EM,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第6个图中共有点的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.
(1)求证:BD=BF;
(2)若AB=10,CD=4,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )

A. 众数是7 B. 中位数是6.5
C. 平均数是 6.5 D. 平均每周锻炼超过6小时的人占总数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
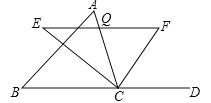
【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五个城市的国际标准时间(单位:时)在数轴上表示如图所示.对应于北京时间2009年1月1日上午9时这一时刻,下列说法错误的是( ).

A.伦敦时间为2009年1月1日凌晨1时
B.纽约时间为2008年12月31日晚上20时
C.圣多明各时间为2008年12月31日晚上22时
D.首尔时间为2009年1月1日上午10时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com