【题目】等腰三角形的底边BC=8cm，且|AC﹣BC|=2cm，则腰长AC的长为（ ）
A. 10cm或6cm B. 10cm C. 6cm D. 8cm或6cm
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】对于点P（x，y），规定x+y=a，那么就把a叫点P的亲和数．例如：若P（2，3），则2+3=5，那么5叫P的亲和数．
（1）在平面直角坐标系中，已知，点A（﹣2，6） ①B（1，3），C（3，2），D（2，2），与点A的亲和数相等的点；
②若点E在直线y=x+6上，且与点A的亲和数相同，则点E的坐标是；
（2）如图点P是矩形GHMN边上的任意点，且点H（2，3），N（﹣2，﹣3），点Q是直线y=﹣x+b上的任意点，若存在两点P、Q的亲和数相同，那么求b的取值范围？ 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】两条平行直线上各有n个点，用这n对点按如下的规则连接线段；
①平行线之间的点在连线段时，可以有共同的端点，但不能有其它交点；
②符合①要求的线段必须全部画出；
图1展示了当n=1时的情况，此时图中三角形的个数为0；
图2展示了当n=2时的一种情况，此时图中三角形的个数为2；
（1）当n=3时，请在图3中画出使三角形个数最少的图形，此时图中三角形的个数为__________个；
（2）试猜想当n对点时，按上述规则画出的图形中，最少有多少个三角形？
（3）当n=2006时，按上述规则画出的图形中，最少有多少个三角形？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为鼓励大学生创业，政府制定了小型企业的优惠政策，许多小型企业应运而生．某市统计了该市2015年1﹣5月新注册小型企业的数量，并将结果绘制成如图两种不完整的统计图：
（1）某市2015年1﹣5月份新注册小型企业一共 家，请将折线统计图补充完整．
（2）该市2015年3月新注册小型企业中，只有2家是养殖企业，现从3月新注册的小型企业中随机抽取2家企业了解其经营情况．请以列表或画树状图的方法求出所抽取的2家企业恰好都是养殖企业的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，如果抛物线y＝2x2不动，而把x轴、y轴分别向下、向右平移2个单位长度，那么在新坐标系下抛物线的解析式为（ ）
A.y＝2（x﹣2）2+2B.y＝2（x+2）2﹣2
C.y＝2（x﹣2）2﹣2D.y＝2（x+2）2+2
查看答案和解析>>
科目：初中数学 来源： 题型：
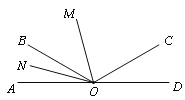
【题目】如图，已知O为直线AD上一点，∠AOC与∠AOB互补，OM、ON分别是∠AOC、∠AOB的平分线，∠MON＝56°.
⑴ ∠COD与∠AOB相等吗？请说明理由；
⑵ 求∠BOC的度数；
⑶ 求∠AOB与∠AOC的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们定义：如图1，在△ABC看，把AB点绕点A顺时针旋转α（0°＜α＜180°）得到AB'，把AC绕点A逆时针旋转β得到AC'，连接B'C'．当α+β=180°时，我们称△A'B'C'是△ABC的“旋补三角形”，△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．
特例感知：
（1）在图2，图3中，△AB'C'是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．
①如图2，当△ABC为等边三角形时，AD与BC的数量关系为AD= BC；
②如图3，当∠BAC=90°，BC=8时，则AD长为 ．
猜想论证：
（2）在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．
拓展应用
（3）如图4，在四边形ABCD，∠C=90°，∠D=150°，BC=12，CD=2
，DA=6．在四边形内部是否存在点P，使△PDC是△PAB的“旋补三角形”？若存在，给予证明，并求△PAB的“旋补中线”长；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
