
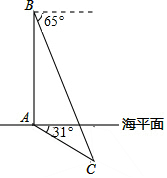
 在某次反潜演习中,红方军舰A测得蓝方潜艇C的俯角为31°,位于军舰A正上方800米的红方反潜直升机B测得潜艇C的俯角为65°.试根据以上数据求出潜艇C离开海平面的下潜深度(结果保留整数)
在某次反潜演习中,红方军舰A测得蓝方潜艇C的俯角为31°,位于军舰A正上方800米的红方反潜直升机B测得潜艇C的俯角为65°.试根据以上数据求出潜艇C离开海平面的下潜深度(结果保留整数)分析 过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,分别在Rt△ACD中表示出CD和在Rt△BCD中表示出BD,从而利用二者之间的关系列出方程求解.
解答  解:过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,
解:过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,
根据题意得:∠ACD=31°,∠BCD=65°,
设AD=x,则BD=BA+AD=800+x,
在Rt△ACD中,CD=$\frac{AD}{tan∠ACD}$=$\frac{x}{tan31°}$,
在Rt△BCD中,BD=CD•tan65°,
∴800+x=$\frac{x}{tan31°}$•tan65°,即800+x≈$\frac{5}{3}$x•$\frac{15}{7}$,
解得:x=$\frac{2800}{9}$≈311米,
∴潜艇C离开海平面的下潜深度为311米.
点评 本题考查了解直角三角形的应用,解题的关键是从题目中抽象出直角三角形并选择合适的边角关系求解.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题
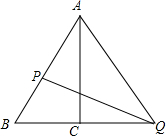 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=6.动点P从点A出发沿AB方向以每秒2个单位的速度运动,同时动点Q从点C出发沿射线BC以每秒2个单位的速度运动,当点P到达点B时,P,Q同时停止运动,连结PQ,QA.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=6.动点P从点A出发沿AB方向以每秒2个单位的速度运动,同时动点Q从点C出发沿射线BC以每秒2个单位的速度运动,当点P到达点B时,P,Q同时停止运动,连结PQ,QA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
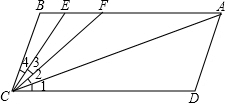 如图,直线AB∥CD,∠B=∠D=120°,E,F在AB上,且∠1=∠2,∠3=∠4
如图,直线AB∥CD,∠B=∠D=120°,E,F在AB上,且∠1=∠2,∠3=∠4查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2=4 | B. | (x-3)2=14 | C. | (x-9)2=4 | D. | (x-9)2=14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=ax2+bx经过点(3,-3),(-1,-3).
已知抛物线y=ax2+bx经过点(3,-3),(-1,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,0) | B. | (a,-b) | C. | (-a,b) | D. | (-a,-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com