

科目:初中数学 来源: 题型:
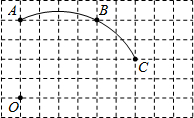 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:
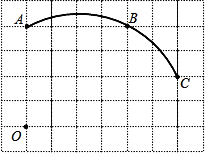 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:
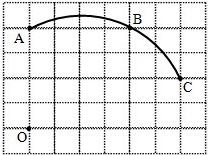
 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年江苏省实验学校九年级上学期期中考试数学卷 题型:解答题
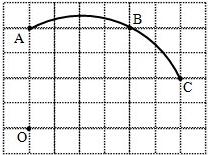
如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
1.请完成如下操作:
①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长,建立平面直角坐标系;②画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连接AD、CD.
2.请在(1)的基础上,完成下列问题:
①写出点的坐标:C _________、D ________;
②⊙D的半径为________ (结果保留根号);
③若扇形ADC是一个圆锥的侧面展开图,则该圆锥的侧面面积为 ____________(结果保留π);
④若E(7,0),试判断直线EC与⊙D的位置关系并说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com