
【题目】如图,有长为24m的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10m).
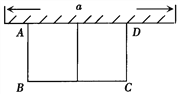
(1)如果所围成的花圃的面积为45m2,试求宽AB的长;
(2)按题目的设计要求,能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
【答案】(1)AB长为5米(2)最大面积为![]()
【解析】试题分析:
(1)由题意可知围成该花圃需要用到篱笆的宽有三条,而长只有一条,设宽AB的长为xm,则长BC为(24-3x)m,再设长方形面积为y,由矩形面积公式可得:y关于x的函数关系式,由y=45解得对应的x的值,可得答案;
(2)把(1)中所得解析式配方化为顶点式,然后结合自变量的取值范围可求得y的最大值,把最大值与45比较可得结论,并进一步可由自变量的取值范围和解析式求得最大面积;
试题解析:
(1)设花圃的宽AB=x米,知BC应为(24-3x)米,故面积y与x的关系式为
y=x(24-3x)=-3x2+24x.
当y=45时,-3x2+24x=45,解出x1=3,x2=5.
当x2=3时,BC=24-3×3>10,不合题意,舍去;
当x2=5时,BC=24-3×5=9,符合题意.
故AB长为5米.
(2)能围成面积比45m2更大的矩形花圃.
由(1)知,y=-3x2+24x=-3(x-4)2+48,
∵![]() ,∴
,∴![]() ,
,
由抛物线y=-3(x-4)2+48知,在对称轴x=4的右侧,y随x的增大而减小,
∴当![]() 时,y=-3(x-4)2+48有最大值,且最大值为
时,y=-3(x-4)2+48有最大值,且最大值为![]() 此时,
此时, ![]() BC=10m,即围成长为10米,宽为
BC=10m,即围成长为10米,宽为![]() 米的矩形ABCD花圃时,其最大面积为
米的矩形ABCD花圃时,其最大面积为![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的斜边
的斜边![]() ,
,![]() .
.
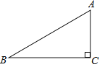
![]() 以点
以点![]() 为圆心作圆,当半径为多长时,直线
为圆心作圆,当半径为多长时,直线![]() 与
与![]() 相切?为什么?
相切?为什么?
![]() 以点
以点![]() 为圆心,分别以
为圆心,分别以![]() 和
和![]() 为半径作两个圆,这两个圆与直线
为半径作两个圆,这两个圆与直线![]() 分别有怎样的位置关系?
分别有怎样的位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生每天参加户外活动的情况,随机抽查了100名学生每天参加户外活动的时间情况,并将抽查结果绘制成如图所示的扇形统计图.
请你根据图中提供的信息解答下列问题:

(1)请直接写出图中![]() 的值,并求出本次抽查中学生每天参加户外活动时间的中位数;
的值,并求出本次抽查中学生每天参加户外活动时间的中位数;
(2)求本次抽查中学生每天参加户外活动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,我们可以利用
,我们可以利用![]() 与
与![]() 相似证明
相似证明![]() ,这个结论我们称之为射影定理,试证明这个定理;
,这个结论我们称之为射影定理,试证明这个定理;
(结论运用)如图![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是对角线
是对角线![]() 、
、![]() 的交点,点
的交点,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
(1)试利用射影定理证明![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
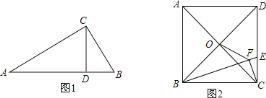
查看答案和解析>>
科目:初中数学 来源: 题型:
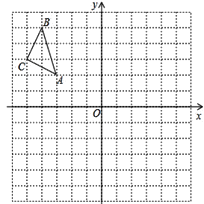
【题目】如图,已知:在平面直角坐标系中,每个小正方形的边长为1,△ABC的顶点都在格点上,点A的坐标为(-3,2).请按要求分别完成下列各小题:
(1)把△ABC向下平移7个单位,再向右平移7个单位,得到△A1B1C1,画出△A1B1C1;
(2)画出△A1B1C1关于x轴对称的△A2B2C2;
画出△A1B1C1关于y轴对称的△A3B3C3;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
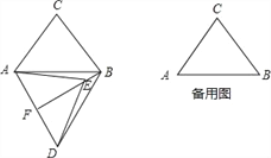
【题目】在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长;
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com