
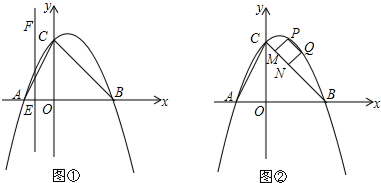
 �躯��y1=��x-k��2+k��y2=��x+k��2-k��ͼ���ཻ�ڵ�A������y1��y2��ͼ��Ķ���ֱ�ΪB��C��
�躯��y1=��x-k��2+k��y2=��x+k��2-k��ͼ���ཻ�ڵ�A������y1��y2��ͼ��Ķ���ֱ�ΪB��C������ ��1��k=0ʱ������y1=y2=x2��k=1ʱ������y1=��x-1��2+1��y2=��x+1��2-1�����ݶ��κ�����ͼ�������ʷֱ����ǵ�ͼ�ɣ�
��2�����ݶ��κ��������ʷֱ������1������������ͼ��Ķ������꣬��Ϻ���ͼ���ֶ�����ֱ��y=x��ͼ���ϣ�
��3����y1=��x-k��2+k����y2=��x+k��2-k�����x��ֵΪ����������֤��x����k�صij����������y����Сֵ��
��4���Ƚ�y=ax+1����y1=��x-k��2+k�������õ�x2-��2k+a��x+k2+k-1=0���ɸ���ϵ���Ĺ�ϵ�ó�AB2=��1+a2����4ka+a2-4k+4����ͬ���õ�CD2=��1+a2����-4ka+a2+4k+4��������AB=CD�ó����̣�1+a2����4ka+a2-4k+4��=��1+a2����-4ka+a2+4k+4�����ⷽ�̼������ʵ��a��ֵ��
��� �⣺��1����ͼ��ʾ��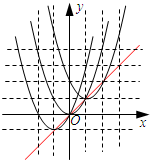
��2������y1=y2=x2�Ķ���Ϊ��0��0����
����y1=��x-1��2+1�Ķ���Ϊ��1��1����
����y2=��x+1��2-1�Ķ���Ϊ��-1��-1����
���Ƕ���ֱ��y=x��ͼ���ϣ���Ϊ���ǵ�������������ʽy=x��
��3����y1=��x-k��2+k����y2=��x+k��2-k��
�ã�x-k��2+k=��x+k��2-k��
������4kx=2k��
�ߺ���y1=��x-k��2+k��y2=��x+k��2-k��ͼ���ཻ�ڵ�A��
��k��0��
���x=$\frac{1}{2}$��
��x����k�صij�����
��ʱy=��$\frac{1}{2}$+k��2-k=k2+$\frac{1}{4}$��$\frac{1}{4}$����y����СֵΪ$\frac{1}{4}$��
��4����y=ax+1����y1=��x-k��2+k��
��ax+1=��x-k��2+k��
������x2-��2k+a��x+k2+k-1=0��
��A��x1��y1����B��x2��y2������y1=ax1+1��y2=ax2+1��
����AB2=��x2-x1��2+��y2-y1��2=��1+a2����x2-x1��2��
�ߣ�x2-x1��2=��x2+x1��2-4x2•x1=��2k+a��2-4��k2+k-1��=4ka+a2-4k+4��
��AB2=��1+a2����4ka+a2-4k+4����
ͬ���õ�CD2=��1+a2����-4ka+a2+4k+4����
��AB=CD��
�ࣨ1+a2����4ka+a2-4k+4��=��1+a2����-4ka+a2+4k+4����
��4ka+a2-4k+4=-4ka+a2+4k+4��
��8ka=8k��
��k��0��
��a=1��
���� �����Ƕ��κ������ۺ����ͣ������漰����֪ʶ���ж��κ�����ͼ�������ʣ���������������������κ�����һԪ���η��̵Ĺ�ϵ����ȷ�����AB2��CD2�ǽ���ڣ�4���ʵĹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У���BAC=90�㣬AB=3��AC=4��BC=5������ABC��ֱ��BC����ƽ��2����λ�õ���DEF������AD�������н��ۣ�
��ͼ���ڡ�ABC�У���BAC=90�㣬AB=3��AC=4��BC=5������ABC��ֱ��BC����ƽ��2����λ�õ���DEF������AD�������н��ۣ�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a�������� | B�� | a�Ƿ���x2-8=0�Ľ� | ||
| C�� | a��8������ƽ���� | D�� | a���㲻��ʽ$\frac{2x-4}{3}��1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ������ABC����ij�г˳���踶����y��Ԫ�����г����x��ǧ�ף�֮��ĺ�����ϵͼ����ij�˸���30.8Ԫ�������ʻ�˶���ǧ�ף�
��ͼ��ʾ������ABC����ij�г˳���踶����y��Ԫ�����г����x��ǧ�ף�֮��ĺ�����ϵͼ����ij�˸���30.8Ԫ�������ʻ�˶���ǧ�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=AC��AD��BC��D�㣬��E��F���߶�AD�ϵ����ȷֵ㣬����BE��CE��BF��CF����$\frac{BC}{AD}=\frac{2}{3}$����BC=4a��
��ͼ���ڡ�ABC�У�AB=AC��AD��BC��D�㣬��E��F���߶�AD�ϵ����ȷֵ㣬����BE��CE��BF��CF����$\frac{BC}{AD}=\frac{2}{3}$����BC=4a���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com