

���� ��1���������߽���ʽ�����A��B�������꣬���������������ο����OC�ij��������C�����꣬�����������ߵĽ���ʽ��
��2������P��PE��x���ڵ�E����BC�ڵ�F������PC����P������Ϊ��m��n����ƽ���ı���BCDP�����ΪS������m��ʾ���ı���BCDP������������ö��κ��������ʿ������ȡ�����ֵʱ��P��D�����ꣻ
��3���ֵ�C����Q����P�ֱ�Ϊֱ�Ƕ��㣬����������ȫ�ȣ��ֱ���⼴�ɣ�
��� �⣺
��1����y=ax2-6ax-16a�У���y=0�ɵ�0=ax2-6ax-16a�����x=-2��x=8��
��A��-2��0����B��8��0����
��OA=2��OB=8��
�ߡ�ACB=90�㣬
���ACO+��OCB=��OCB+��CBO=90�㣬
���ACO=��CBO��
���AOC�ס�COB��
��$\frac{AO}{OC}$=$\frac{OC}{OB}$����OC2=OA•OB=2��8=16��
��OC=4��
��C��0��4����
��-16a=4�����a=-$\frac{1}{4}$��
�������ߵĽ���ʽΪ$y=-\frac{1}{4}{x^2}+\frac{3}{2}x+4$��
��2������P��PE��x���ڵ�E����BC�ڵ�F������PC����ͼ1��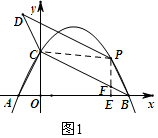
��P������Ϊ��m��n����ƽ���ı���BCDP�����ΪS��
��$PE=n=-\frac{1}{4}{m^2}+\frac{3}{2}m+4$��OE=m��BE=8-m��
�ߡ�COB=��FEB=90�㣬��CBO=��FBE��
���BEF�ס�BOC��
��$\frac{EF}{OC}$=$\frac{BE}{OB}$��
��EF=$\frac{OC•BE}{OB}$=-$\frac{1}{2}$m+4��
��PF=PE-EF=-$\frac{1}{4}$m2+2m��
��S=2S��PBC=2��S��PFC+S��PFB��=2��$\frac{1}{2}$PF•OE+$\frac{1}{2}$PF•BE��=PF•OB=8PF=-2m2+16m=-2��m-4��2+32��
��-2��0��
�൱m=4ʱ��ƽ���ı���BCDP�����S���ʱ$n=-\frac{1}{4}{m^2}+\frac{3}{2}m+4=6$��
��P�������Ϊ��4��6������ƽ�ƿɵô�ʱD�������Ϊ��-4��10����
��3��������P��C��QΪ�����������Ϊ����ֱ�������Σ�
����CΪֱ�Ƕ���ʱ����ͼ2��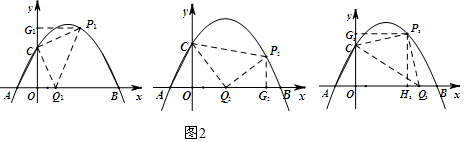
��P1��P1G1��y���ڵ�G1�����֤�á�COQ1�ա�P1G1C��
��P1G1=OC=4��
��P1��4��6������CG1=OQ1=2��
��Q1��2��0����
��QΪֱ�Ƕ���͵�PΪֱ�Ƕ���ʱ��ͬ�������P2��$1+\sqrt{33}$��$-3+\sqrt{33}$����Q2��$-3+\sqrt{33}$��0����P3��$1+\sqrt{17}$��$1+\sqrt{17}$����Q3��$-2+2\sqrt{17}$��0����
���Ͽ�֪�������������ĵ�P��Q��������ΪP1��4��6����Q1��2��0����P2��$1+\sqrt{33}$��$-3+\sqrt{33}$����Q2��$-3+\sqrt{33}$��0����P3��$1+\sqrt{17}$��$1+\sqrt{17}$����Q3��$-2+2\sqrt{17}$��0����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ���������������ε��ж������ʡ�ƽ���ı��ε����ʡ�����ֱ�������ε����ʡ����κ��������ʡ�����˼��ͷ�������˼�룮�ڣ�1�������A��B��C��������ǽ���Ĺؼ����ڣ�2���У���m��ʾ���ı���BCDP������ǽ���Ĺؼ����ڣ�3���з���������ֱ���������ȫ���ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
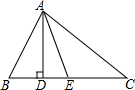 ��ͼ�ڡ�ABC�У�AD��BC��AEƽ�֡�BAC����B=80�㣬��C=40�㣬���BAE=30�㣻��DAE=20�㣮
��ͼ�ڡ�ABC�У�AD��BC��AEƽ�֡�BAC����B=80�㣬��C=40�㣬���BAE=30�㣻��DAE=20�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
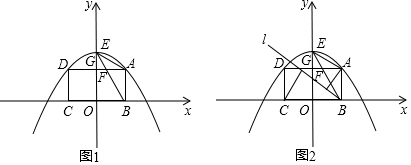
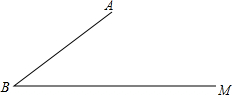 ��ͼ����֪��ABM=37�㣬AB=20��C������BM��һ�㣮
��ͼ����֪��ABM=37�㣬AB=20��C������BM��һ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
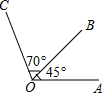 ��֪����ͼ����AOB=45�㣬��BOC=70�㣬���AOC�Ķ�����
��֪����ͼ����AOB=45�㣬��BOC=70�㣬���AOC�Ķ������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com