
����Ŀ��Ϊ����ѧ����չ��Ұ���ḻ֪ʶ����������Ȼ���Ļ�������,���ӶԼ������ʽ����ṫ�����µ�����,����ij��ѧ������֯����ʦ��ȥ�����۹��↑չ��ѧ���л.�ڲμӴ˴λ��ʦ����,��ÿλ��ʦ��![]() ��ѧ��,��ʣ
��ѧ��,��ʣ![]() ��ѧ��û�˴�;��ÿλ��ʦ��
��ѧ��û�˴�;��ÿλ��ʦ��![]() ��ѧ��������һλ��ʦ�ٴ�
��ѧ��������һλ��ʦ�ٴ�![]() ��ѧ��.Ϊ�˰�ȫ,��Ҫ��֤����ʦ�����г���,��Ҫ��֤ÿ���ͳ�������Ҫ��
��ѧ��.Ϊ�˰�ȫ,��Ҫ��֤����ʦ�����г���,��Ҫ��֤ÿ���ͳ�������Ҫ��![]() ����ʦ.���мס������ִ�ͳ������ǵ��ؿ�������������ʾ.
����ʦ.���мס������ִ�ͳ������ǵ��ؿ�������������ʾ.

��1���μӴ˴���ѧ���л����ʦ�� �ˣ�ѧ���� �ˣ����ÿͳ�����Ϊ ����
��2��������![]() �����ֿͳ��������Ϊ
�����ֿͳ��������Ϊ![]() Ԫ����д��
Ԫ����д��![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3���ڣ�2���������£�ѧУ�ƻ��˴���ѧ���л����ܷ��ò�����![]() Ԫ�����ܵó��ļ��ֲ�ͬ������������������������ʡǮ����˵������.
Ԫ�����ܵó��ļ��ֲ�ͬ������������������������ʡǮ����˵������.
���𰸡���1��![]() ��
��![]() ��
��![]() ����2��
����2��![]() ����3������
����3������![]() �������������һ�����ü��ֿͳ�
�������������һ�����ü��ֿͳ�![]() �������ֿͳ�
�������ֿͳ�![]() ���������������ü��ֿͳ�
���������������ü��ֿͳ�![]() �������ֿͳ�
�������ֿͳ�![]() ���������������ü��ֿͳ�
���������������ü��ֿͳ�![]() �������ֿͳ�
�������ֿͳ�![]() �������ʡ���õ�������ǣ����ü��ֿͳ�
�������ʡ���õ�������ǣ����ü��ֿͳ�![]() �������ֿͳ�
�������ֿͳ�![]() ����
����
��������
��1�������ʦ��x����ѧ����y�����ó���Ԫһ�η����飬������ɣ�
��2������![]() ���ң�����ֿͳ���Ϊ��
���ң�����ֿͳ���Ϊ��![]() ����������㼴��
����������㼴��
��3��������x�����ֿͳ�������ֿͳ���Ϊ����8-x������������ó�400x+300��8-x����3100���ó�xȡֵ��Χ�������ó����ɣ�
(1)����ʦ��x����ѧ����y����
�����⣬�з�����![]() ��
��
���![]() ��
��
��ÿ���ͳ�������Ҫ��2����ʦ��
�������������ܳ���8����
��Ҫ��֤300��ʦ���г���,������������С��![]() =
=![]() (ȡ��Ϊ8)����
(ȡ��Ϊ8)����
�ۺ�������֪��������Ϊ8����
����ʦ��16����ѧ����284�������ÿͳ�����Ϊ8����
��2��![]() ����
����![]() ���ң�
���ң�![]() ���ֿͳ���Ϊ��
���ֿͳ���Ϊ��![]() ����
����
![]() .
.
��3��![]() ��ܷ��ò�����
��ܷ��ò�����![]() Ԫ���������ֿͳ�������
Ԫ���������ֿͳ�������![]() ����
����
![]() ����ã�
����ã�![]() ��
��
Ϊʹ![]() ��ʦ����������
��ʦ����������![]() ��
��
��ã�![]() ��
��
![]() ȡ����Ϊ
ȡ����Ϊ![]() .
.
![]() ����
����![]() ���������
���������
����һ�����ü��ֿͳ�![]() �������ֿͳ�
�������ֿͳ�![]() ����
����
�����������ü��ֿͳ�![]() �������ֿͳ�
�������ֿͳ�![]() ����
����
�����������ü��ֿͳ�![]() �������ֿͳ�
�������ֿͳ�![]() ����
����
�ɣ�2��![]() ��
��![]() ��
��![]() �ļ�С����С��
�ļ�С����С��
![]() ��
��![]() ������
������![]() ��
��![]() ʱ��
ʱ��![]() Ԫ��
Ԫ��
�����ʡ���õ�������ǣ����ü��ֿͳ�![]() �������ֿͳ�
�������ֿͳ�![]() ����
����


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʽ![]() ��ʵ����Χ�ڳ���������a��x��y��������ͬ��ʵ������
��ʵ����Χ�ڳ���������a��x��y��������ͬ��ʵ������![]() ��ֵ��(����)
��ֵ��(����)
A. 3 B. ![]() C. 2 D.
C. 2 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶���б�ҵ������Ҫ�Ӿţ�1�����2������1��Ů�����ţ�2����1������1��Ů����5����ѡ��2�������ˣ�
��1��������ͼ���б����г����п������Σ�
��2����2�����������Բ�ͬ�༶�ĸ��ʣ�
��3����2��������ǡ��1��1Ů�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
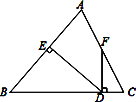
����Ŀ����ͼ��ʾ����ABC�У�AB=BC��DE��AB�ڵ�E��DF��BC�ڵ�D����AC��F��
������AFD=155�������EDF�Ķ�����
������F��AC���е㣬��֤����CFD=![]() ��B��
��B��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
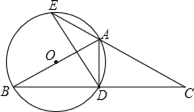
����Ŀ����ͼ����ABC�У�AB=AC����ABΪֱ������O����BC�ڵ�D����CA���ӳ����ڵ�E������AD��DE��
��1����֤��D��BC���е㣻
��2����DE=3��BD��AD=2�����O�İ뾶��
��3���ڣ�2���������£�����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬BE��AC������Ϊ��F�����������ĸ����ۣ��١�AEF�ס�CAB����CF=2AF����S��ABF��S�ı���CDEF=2��5����cos��CAD=![]() ��������ȷ�Ľ����У���������
��������ȷ�Ľ����У���������
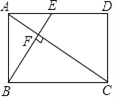
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
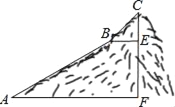
����Ŀ����ͼ��Ϊ����һ��ɽ��CF�ĸ߶ȣ�����ɽ��ij��ɽ�»���ΪAB��BC���Σ�ÿһ��ɽ�½����ǡ�ֱ���ģ�����³�AB=800�ף�BC=200�ף��½ǡ�BAF=30�㣬��CBE=45�㣮
��1����AB��ɽ�µĸ߶�EF��
��2����ɽ��ĸ߶�CF�����������ʽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڷ����¹�״�����ڼ䣬�����ҽ�ÿ��ֵ�����Խ��Խ��.ijҩ���һ����2000Ԫ����ҽ�ÿ������ɸ����ڶ�������2000Ԫ�����ÿ���֣����ڶ���ÿ�����ֵĽ����ǵ�һ�ν��۵�1.25���������������ȵ�һ����200��.
�����һ�κ͵ڶ��ηֱ���ҽ�ÿ�������Ϊ���ٸ���
��ҩ���һ�ι������ֺ�����ÿ��3Ԫ�ļ۸���ۣ�������a�����ڶ���ͬ���֣����ڽ�������ˣ�ҩ�꽫���ֵ��ۼ�Ҳ������ÿ��3.5Ԫ��������������b�������ι�����4800Ԫ.��ҽԺҽ�����ʽ�ȱ��ҩ�������ʣ��Ŀ���ȫ��������ҽԺ.����ҩ��������������ж��ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���E��F�ֱ���AD��BC���е㣬�ֱ�����BE��DF��BD��
��1����֤����AEB�ա�CFD��
��2������ABD����ʲô����ʱ���ı���EBFD�����Σ���˵�����ɣ�
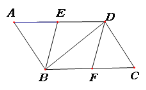
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com