
����Ŀ����ƽ��ֱ������ϵxOy�е�ijԲ�ϣ�����MN��ȡMN���е�P�����ǹ涨:��P��ij�㣨ֱ�ߣ��ľ�����������оࡱ���÷��š�![]() ����ʾ.
����ʾ.
��������W��-3��0��ΪԲ�ģ��뾶Ϊ2����WԲ�����������������������������
��1����֪��MN����Ϊ2.
����ͼ1����MN��x��ʱ��ֱ��д����ԭ��O��![]() �ij��ȣ�
�ij��ȣ�
�����MN��Բ���˶�ʱ����ͼ2�л���ʾ��ͼ����ֱ��д������O��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��2����֪��![]() ,��NΪ��W�ϵ�һ���㣬��ֱ��
,��NΪ��W�ϵ�һ���㣬��ֱ��![]() ����ֱ��
����ֱ��![]() ��
��![]() �����ֵ.
�����ֵ.
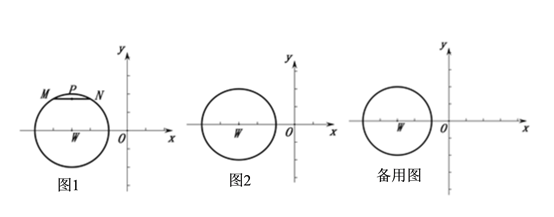
���𰸡���1����![]() ����
����![]() ����2��d�������ֵΪ
����2��d�������ֵΪ![]() .
.
��������
��1������ͼ3������PW��OP��MW������֪��PW=![]() ����PWO=90�㣬OW=3��������Rt��PWO���ɹ��ɶ���������ô�ʱ��P��ԭ��O�����о�d��=
����PWO=90�㣬OW=3��������Rt��PWO���ɹ��ɶ���������ô�ʱ��P��ԭ��O�����о�d��=![]() �����������֪������MN�ڡ�W���˶�ʱ����P���˶�·�����Ե�WΪԲ�ģ�PWΪ�뾶��Բ����ͼ4��������Ӧ��ͼ�Σ���ͼ���PW=
�����������֪������MN�ڡ�W���˶�ʱ����P���˶�·�����Ե�WΪԲ�ģ�PWΪ�뾶��Բ����ͼ4��������Ӧ��ͼ�Σ���ͼ���PW=![]() �����ɵõ���ʱ��P��ԭ��O�����о�d����ȡֵ��Χ�ˣ�
�����ɵõ���ʱ��P��ԭ��O�����о�d����ȡֵ��Χ�ˣ�
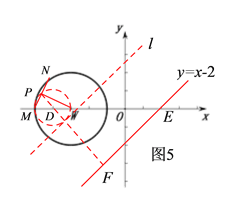
��2���������õ���N�ڡ�W���˶�ʱ����P����DΪԲ�ģ�WMΪֱ����Բ���˶����ɴ˻������������ͼ����ͼ5����ֱ��lƽ����ֱ��y=x-2������ͼ��֪����ֱ��l����D���У������о�d����Բ��Dʱ����P��ֱ��l�����о�d��������ʱ��P��ֱ��y=x-2�����о�Ҳ������������֪�������м��㼴����������ֵ��.
��1������ͼ3������PW��OP��MW��
����P��MN���е㣬MN=2��
��PW��MN��MP=1��
��MN��x����
��PW��x����
���PWO=90�㣬
��OW=3��
����Rt��PWO��PO=![]() ��
��
����ʱ��P��ԭ��O�����оࣺd��=![]() ��
��
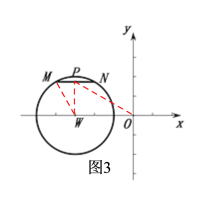
���������֪������MN�ڡ�W���˶�ʱ����P���˶�·�����Ե�WΪԲ�ģ�PWΪ�뾶��Բ����ͼ4��
��PW=![]() ��OW=3��
��OW=3��
����ʱ��P��ԭ��O�����о�d����ȡֵ��ΧΪ��![]() <d��<
<d��<![]() ��
��

��2����ͼ5����P����MN���е㣬
��WP��MN��
������N�ڡ�W���˶�ʱ����P����DΪԲ�ģ�WMΪֱ����Բ���˶���
��W��������-3��0������M��������-5��0����
����D��������-4��0����
��ֱ��lƽ����ֱ��y=x-2����P��ֱ��l�����о����ʱ����P��ֱ��y=x-2�����о�����
��ͼ��֪����ֱ��l����D���У������о�d����Բ��Dʱ����P��ֱ��l�����о�d�����
��ֱ��y=x-2��x�ύ�ڵ�E������D��ֱ��y=x-2�Ĵ��߽�ֱ���ڵ�F��
��ֱ��y=x-2��x���ཻ�γɵ����Ϊ45�㣬��E������Ϊ��2��0����
��DE=6��
��DF=DE��sin45��=![]() ������ʱֱ��l��ֱ��y=x-2�ľ���Ϊ
������ʱֱ��l��ֱ��y=x-2�ľ���Ϊ![]() ��
��
����P��ֱ��y=x-2��������Ϊ��![]() ����d�������ֵΪ��
����d�������ֵΪ��![]() .
.


 �������ͬ������ϵ�д�
�������ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������1��3��5��7����������һ�������ų������
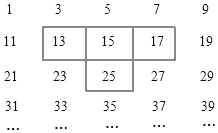
ͼ�е�T�ֿ��ס���ĸ����֣�����T�ֿ����������ƶ�����ͬ���ķ�ʽ�ɿ�ס������ĸ���, ����T�ֿ����������ƶ������ס���ĸ����ĺͲ����ܵõ������ǣ� ��
A.22B.70C.182D.206
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
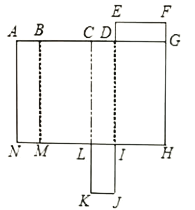
����Ŀ����ͼ��ʾ�dz������ƽ��չ��ͼ����![]() ����
����![]() ��
��
��1������![]() ���ܳ��볤����
���ܳ��볤����![]() ���ܳ�(����ĸ
���ܳ�(����ĸ![]() ���б�ʾ) ��
���б�ʾ) ��
��2����������![]() ���ܳ��ȳ�����
���ܳ��ȳ�����![]() ���ܳ���8����ԭ������������
���ܳ���8����ԭ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������������������![]() ��
��![]() �������������εĿ�����2����λ���ȣ�������
�������������εĿ�����2����λ���ȣ�������![]() �ij�
�ij�![]() ��4����λ���ȣ�������
��4����λ���ȣ�������![]() �ij�
�ij�![]() ��8����λ���ȣ���
��8����λ���ȣ���![]() �������ϱ�ʾ������5����
�������ϱ�ʾ������5����![]() ����֮��ľ���Ϊ12��
����֮��ľ���Ϊ12��

��1�����:��![]() �������ϱ�ʾ������_________ ����
�������ϱ�ʾ������_________ ����![]() �������ϱ�ʾ������_________��
�������ϱ�ʾ������_________��
��2�����߶�![]() ���е�Ϊ
���е�Ϊ![]() ���߶�EH����һ��
���߶�EH����һ��![]() ��
��![]() ��
�� ![]() ��ÿ��4����λ���ٶ����������˶���
��ÿ��4����λ���ٶ����������˶���![]() ��ÿ��3����λ���ٶ������˶������˶�ʱ��Ϊ
��ÿ��3����λ���ٶ������˶������˶�ʱ��Ϊ![]() �룬��
�룬��![]() ������ʱ��
������ʱ��![]() ��
��
��3����������![]() ��ÿ��2����λ���ٶ����������˶���������
��ÿ��2����λ���ٶ����������˶���������![]() �̶��������������������ص����ֵ����Ϊ6ʱ������
�̶��������������������ص����ֵ����Ϊ6ʱ������![]() �˶���ʱ�䣮
�˶���ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η���ax2+bx��1��0��a��0����һ��Ϊx��2019����һԪ���η���a��x��1��2+b��x��1����1����һ��Ϊ��������
A.![]() B.2020C.2019D.2018
B.2020C.2019D.2018
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������M��O��N��Ӧ�����ֱ�Ϊ��1��0��3����PΪ����������һ�������Ӧ����Ϊx��
![]()
��1��MN�ij�Ϊ ��
��2�������P����M����N�ľ����������ôx��ֵ�� ��
��3���������Ƿ���ڵ�P��ʹ��P����M����N�ľ���֮����8����������ֱ��д��x��ֵ��������������˵��������
��4�������P��ÿ����1����λ���ȵ��ٶȴӵ�O�����˶���ͬʱ��M�͵�N�ֱ���ÿ����2����λ���Ⱥ�ÿ����3����λ���ȵ��ٶ�Ҳ�����˶�����t����ʱ��P����M����N�ľ����������t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
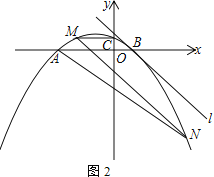
����Ŀ����֪��������y��a(x��m)(x��3m)��a��0��m��0����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C��ֱ��l��y��kx��b������B���������������Ψһ�����㣬ƽ��ֱ��l����������M��N���㣨��M��N�ֱ�λ��x���Ϸ����·���
(1) ��![]() ��C(0��
��C(0��![]() )
)
�� ��������ߵĽ���ʽ
�� ��ͼ1������AM��AN����֤����MAB����NAB
(2) ��ͼ2������MC����MC��x�ᣬ��![]() ��ֵ
��ֵ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˹��������Լ��ˮ��ij������ˮ��˾�����·�ʽ��ÿ������ˮ�����м��㣺����ˮ��������![]() ��ʱ��ÿ�����շѱ�Ϊ
��ʱ��ÿ�����շѱ�Ϊ![]() Ԫ������ˮ������
Ԫ������ˮ������![]() ��ʱ������
��ʱ������![]() ���IJ���ÿ�����շѱ�Ϊ
���IJ���ÿ�����շѱ�Ϊ![]() Ԫ���±���С����
Ԫ���±���С����![]() �·���ˮ���ͽ��������
�·���ˮ���ͽ��������
�·� |
|
|
|
|
��ˮ�������� |
|
|
|
|
���ã�Ԫ�� |
|
|
|
|
����ݱ������ṩ����Ϣ���ش��������⣺
��1��![]() ___________��
___________��![]() ____________��
____________��
��2����С����![]() �·ݽ���ˮ��
�·ݽ���ˮ��![]() Ԫ����С����
Ԫ����С����![]() �·���ˮ���ٷ���
�·���ˮ���ٷ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һԪһ�η��̽�Ӧ���⣺
2019��6����������۸��߸ߣ������������������ĸ߶ȹ�ע���г�����ĵ����ǵ�ÿǧ��50Ԫʱ����������Ͷ�봢��������ƽ������۸�2019��12�£�����Ͷ�Ŵ�������4��֣�Ͷ�ź����ڿ�ʼ�����ɹ���ij����Ҳ������Ӧ�Ĵ�������£�
һ���Թ���������ǧ�ˣ� | ������� |
������20ǧ�� | һ�ɰ��ۼ۷��� |
����20ǧ�ˣ���������40ǧ�� | һ�ɰ��ۼ۷��� |
����40ǧ�� | �����ۼ۷��� |
���磺ij�˿�����45ǧ�����⣬��ʵ�ʸ���Ϊ��![]() ��Ԫ����
��Ԫ����
��1���ó����ڴ���ǰ������һ�����⣬����ǰ��ÿǧ��50Ԫ�ĵ�������10ǧ�ˣ������ڼ���ͬ���ĵ�������30ǧ�˸�С���ң�������֣�����ǰ������10ǧ�������õ����������С���ҵ�30ǧ�������õ�����һ���࣬��ó��й�����������Ľ���Ϊÿǧ�˶���Ԫ��
��2�������ڼ䣬С��ҴӸó�����ÿǧ��50Ԫ�ĵ��۷����ι���������80ǧ�ˣ���һ�ι�����������ڵڶ��ι����������������ʵ�ʹ�����2990Ԫ����С������ηֱ����������ǧ�ˣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com