
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2﹣4ac>0;②abc>0;③a+c>0;④9a+3b+c<0.其中,正确的结论有( )
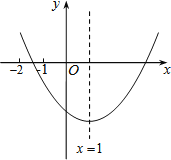
A.4个B.3个C.2个D.1个
【答案】B
【解析】
根据抛物线与x轴有两个交点对①进行判断;由抛物线开口方向得到a>0,由抛物线对称轴为直线x=﹣![]() =1得到b=﹣2a,b<0,由抛物线与y轴的交点在x轴下方得到c<0,则可对②进行判断;根据x=﹣1时,y<0,则a﹣b+c<0,即a+c<b,这样可对③进行判断;根据抛物线的对称性可得到抛物线与x轴的另一个交点在(3,0)和(4,0)之间,则x=3时,y<0,即9a+3b+c<0,则可对④进行判断.
=1得到b=﹣2a,b<0,由抛物线与y轴的交点在x轴下方得到c<0,则可对②进行判断;根据x=﹣1时,y<0,则a﹣b+c<0,即a+c<b,这样可对③进行判断;根据抛物线的对称性可得到抛物线与x轴的另一个交点在(3,0)和(4,0)之间,则x=3时,y<0,即9a+3b+c<0,则可对④进行判断.
解:∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,所以①正确;
∵抛物线开口向上,
∴a>0,
又∵抛物线对称轴为直线x=﹣![]() =1,
=1,
∴b=﹣2a,b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以②正确;
∵x=﹣1时,y<0,即a﹣b+c<0,
∴a+c<b<0,所以③错误;
∵抛物线对称轴为直线x=1,而抛物线与x轴的一个交点在(﹣2,0)和(﹣1,0)在之间,
∴抛物线与x轴的另一个交点在(3,0)和(4,0)之间,
∴当x=3时,y<0,即9a+3b+c<0,所以④正确.
故选:B.


科目:初中数学 来源: 题型:
【题目】马路两侧有两根灯杆AB、CD,当小明站在点N处时,在灯C的照射下小明的影长正好为NB,在灯A的照射下小明的影长为NE,测得BD=24m,NB=6m,NE=2m.
(1)若小明的身高MN=1.6m,求AB的长;
(2)试判断这两根灯杆的高度是否相等,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北山水果市场是我区最大的水果批发市场,张老师想购买甲、乙、丙三种水果,如果购买甲2千克,乙1千克,丙4千克,共需付钱36元:如果购买甲4千克,乙2千克,丙2千克,共需付钱32元.今要购买甲4千克,乙2千克,丙5千克,则共应付_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c的图象与x轴交于A(2,0),B(﹣8,0)两点,与y轴交于点C(0,﹣8).
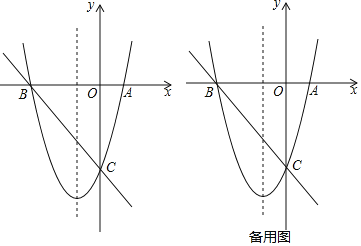
(1)求抛物线的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,求出点F的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
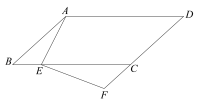
【题目】如图,在□ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD申CD边上任意一点.
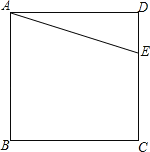
(1)以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形;
(2)在BC边上画一点F,使△CFE的周长等于正方形ABCD的周长的一半,请简要说明你取该点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
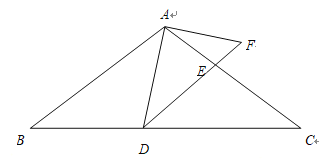
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点(点
边上的一个动点(点![]() 不与点
不与点![]() 、点
、点![]() 重合).以
重合).以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)当![]() 平分
平分![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
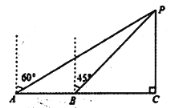
【题目】一艘货轮由西向东航行,在![]() 处测得灯塔
处测得灯塔![]() 在它的北偏东60°方向,继续航行到达
在它的北偏东60°方向,继续航行到达![]() 处,测得灯塔
处,测得灯塔![]() 在正南方向10海里的
在正南方向10海里的![]() 处是港口,点
处是港口,点![]() 、
、![]() 、
、![]() 在一条直线上,则这艘货轮由
在一条直线上,则这艘货轮由![]() 处到
处到![]() 处航行的路程为__________海里(结果保留根号).
处航行的路程为__________海里(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com