
分析 ①根据题意,以及根与系数的关系,可知两个整数根都是负数;②根据根的判别式,以及题意可以得出a2-2b≥0以及b2-2a≥0,进而得解.
解答 解:①两个整数根且乘积为正,两个根同号,由韦达定理有,x1•x2=2b>0,y1•y2=2a>0,
y1+y2=-2b<0,
x1+x2=-2a<0,
这两个方程的根都为负根,①正确;
②由根判别式有:
△=4a2-8b≥0,△=4b2-8a≥0,
∵4a2-8b≥0,4b2-8a≥0,
∴a2-2b≥0,b2-2a≥0,
a2-2a+1+b2-2b+1=a2-2b+b2-2a+2≥2,
(a-1)2+(b-1)2≥2,②正确;
故答案为:①②.
点评 本题主要考查了根与系数的关系,以及一元二次方程的根的判别式,综合运用知识是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示.
某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示.| 测试 项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将45°的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺的下沿重合,OB与尺上沿的交点B在尺上的度数为2cm,若将射线OB绕点O顺时针旋转18°与尺子的上沿交于点C,则点C在尺上的度数约为3.9cm.(结果精确到0.1cm,参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
如图,将45°的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺的下沿重合,OB与尺上沿的交点B在尺上的度数为2cm,若将射线OB绕点O顺时针旋转18°与尺子的上沿交于点C,则点C在尺上的度数约为3.9cm.(结果精确到0.1cm,参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
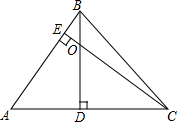 若∠BAC是△ABC的最大内角,△ABC的高BD、CE所在的直线相交于点O,点D、E都不与点A重合.猜想∠BAC和∠COD有何数量关系?请画出相应的图形,并证明你的结论.
若∠BAC是△ABC的最大内角,△ABC的高BD、CE所在的直线相交于点O,点D、E都不与点A重合.猜想∠BAC和∠COD有何数量关系?请画出相应的图形,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
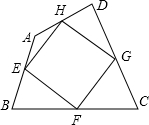 已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,当四边形ABCD的对角线AC、BD满足AC=BD时,四边形EFGH是菱形.
已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,当四边形ABCD的对角线AC、BD满足AC=BD时,四边形EFGH是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.
如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com