
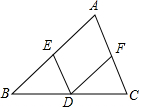
 在△ABC中,点D、E、F分别是BC、AB、AC边的中点.求证:△BED≌△DFC.
在△ABC中,点D、E、F分别是BC、AB、AC边的中点.求证:△BED≌△DFC. 分析 先根据三角形中位线定理得出∠EDB=∠C,∠B=∠FDC,再由F是AC边的中点得出FC=$\frac{1}{2}$AC,
故可得出DE=FC,利用AAS定理即可得出结论.
解答 证明:∵点D、E分别是BC、AB的中点,
∴ED∥AC,ED=$\frac{1}{2}$AC,
∴∠EDB=∠C.
又∵F是AC边的中点,
∴FC=$\frac{1}{2}$AC,
∴DE=FC,
同理可得,∠B=∠FDC,
在△EBD和△FDC中,
∵$\left\{\begin{array}{l}{∠B=∠FDC}\\{∠EDC=∠C}\\{ED=FC}\end{array}\right.$,
∴△BED≌△DFC(AAS).
点评 本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:解答题
 某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多17个.
某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多17个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查你所在的班级同学的身高情况 | B. | 调查全国中学生心理健康现状 | ||
| C. | 调查我市食品合格情况 | D. | 调查中央电视台《少儿节目》收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com