
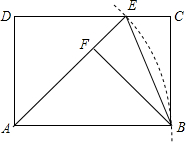
 如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F.
如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F.分析 (1)利用矩形的性质得出AB∥DC,∠D=90°,再利用全等三角形的判定得出△ABF≌△ADE进而得出答案;
(2)根据等腰三角形的性质得到∠AEB=∠ABE=67.5°,由三角形的内角和得到∠EAB=45°,推出△ADE是等腰直角三角形,得到AD=AE,根据等腰直角三角形的性质列方程得到AE=2,于是得到结论.
解答 (1)证明:在矩形ABCD中,AB∥DC,∠D=90°,
∴∠AED=∠FAB,
∵BF⊥AE,
∴∠AFB=∠D=90°,
由作图可知,AB=AE,
在△ABF和△ADE中,
$\left\{\begin{array}{l}{∠D=∠AFB}\\{∠AED=∠FAB}\\{AE=AB}\end{array}\right.$,
∴△ABF≌△ADE(AAS),
∴BF=AD;
(2)解:∵AE=AB,
∴∠AEB=∠ABE=67.5°,
∴∠EAB=45°,
∴∠DEA=45°,
∴△ADE是等腰直角三角形,
∴AD=AE,
设AE=x,则DE=x-$\sqrt{2}$+1,
∴x=$\sqrt{2}$(x-$\sqrt{2}$+1),
∴x=$\sqrt{2}$,
∴AE=$\sqrt{2}$,
∴扇形ABE的面积=$\frac{45×π×({\sqrt{2})}^{2}}{360}$=$\frac{1}{4}$π.
点评 此题主要考查了全等三角形的判定与性质以及矩形的性质,扇形的面积的计算,得出△ABF≌△ADE是解题关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
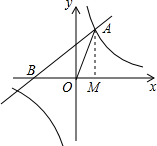 已知:如图,一次函数$y=\frac{{\sqrt{3}}}{3}x+m$与反比例函数$y=\frac{{\sqrt{3}}}{x}$的图象在第一象限的交点为A(1,n).
已知:如图,一次函数$y=\frac{{\sqrt{3}}}{3}x+m$与反比例函数$y=\frac{{\sqrt{3}}}{x}$的图象在第一象限的交点为A(1,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周进行体育锻炼的时间 | |
| B. | 对旅客上飞机前进行的安检 | |
| C. | 学校招聘教师,对应聘人员进行面试 | |
| D. | 了解全市中小学生每天的零花钱 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
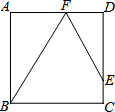 已知如图,正方形ABCD中,AD=4,点E在CD上,DE=3CE,F是AD上异于D的点,且∠EFB=∠FBC,则tan∠DFE=$\frac{15}{8}$.
已知如图,正方形ABCD中,AD=4,点E在CD上,DE=3CE,F是AD上异于D的点,且∠EFB=∠FBC,则tan∠DFE=$\frac{15}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
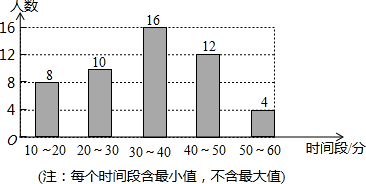 某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.
某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
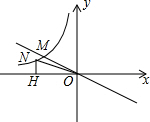 如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H.
如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某广场的形状是正方形,可以用64块地砖铺满,设计人员打算用黑、白两种颜色的地砖来铺,并且使上空的一只小鸽子随机地落在广场上时,落在黑色地砖上的概率是$\frac{11}{32}$,请你帮助设计人员设计一种铺设地砖的方案.(把铺褐色地砖的地方涂黑,使设计的图案美观,且是轴对称图形)
如图,某广场的形状是正方形,可以用64块地砖铺满,设计人员打算用黑、白两种颜色的地砖来铺,并且使上空的一只小鸽子随机地落在广场上时,落在黑色地砖上的概率是$\frac{11}{32}$,请你帮助设计人员设计一种铺设地砖的方案.(把铺褐色地砖的地方涂黑,使设计的图案美观,且是轴对称图形)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com