
分析 (1)假设存在,根据等比函数定义得出b2=9,继而可得b的值,从而得出解析式;
(2)根据等比函数定义及b<0得出b2=9c,即b=-3 $\sqrt{c}$,根据“等比”函数的图象与y=-$\frac{c}{x}$的图象的交点的横坐标为x=-$\frac{1}{3}$,列出方程即可解决问题.
(3)存在,由题意b2=ac,且a=3b,推出b2=3bc,因为a>0,c>0,所以b=3c,a=9c,则一次函数解析式为y=9cx+3c,“等比”函数解析式为y=9cx2+3cx+c,即9x2-6x-2=0,可得x1+x2=$\frac{2}{3}$,x1x2=-$\frac{2}{9}$,|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(\frac{2}{3})^{2}-4×(-\frac{2}{9})}$=$\frac{2}{3}$$\sqrt{3}$,再构建二次函数,利用二次函数的性质即可解决问题.
解答 解:(1)存在,
假设一次函数y=x+b与反比例函数y=-$\frac{9}{x}$存在“等比”函数,则b2=9,
解得:b=3或-3,
∴存在“等比”函数,其解析式为y=x2+3x+9或y=x2-3x+9;
(2)根据题意知,b2=9c,
∴b=±3 $\sqrt{c}$,
∵b<0,
∴b=-3 $\sqrt{c}$,
则“等比”函数的解析式为y=9x2-3 $\sqrt{c}$x+c,
根据题意,x=-$\frac{1}{3}$时,9x2-3 $\sqrt{c}$x+c=-$\frac{c}{x}$,
∴1+$\sqrt{c}$+c=3c,即( $\sqrt{c}$-1)(2 $\sqrt{c}$+1)=0,
解得:$\sqrt{c}$=1,
∴c=1,
故反比例函数的解析式为y=-$\frac{1}{x}$;
(3)存在,
∵b2=ac,且a=3b,
∴b2=3bc,
∵a>0,c>0,
∴b=3c,a=9c,
则一次函数解析式为y=9cx+3c,“等比”函数解析式为y=9cx2+3cx+c,
由9cx2+3cx+c=9cx+3c化简得:9x2-6x-2=0,
∴x1+x2=$\frac{2}{3}$,x1x2=-$\frac{2}{9}$,
∴|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(\frac{2}{3})^{2}-4×(-\frac{2}{9})}$=$\frac{2}{3}$$\sqrt{3}$,
如图,过点P作PH⊥x轴,交AB于H,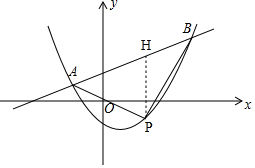
∴H(x,9cx+3c)、P(x,9cx2+3cx+c),
∴PH=9cx+3c-(9cx2+3cx+c)=-c(9x2-6x-2),
∴S=$\frac{1}{2}$PH•|x1-x2|=-$\frac{\sqrt{3}}{3}$c(9x2-6x-2)=-3$\sqrt{3}$c(x-$\frac{1}{3}$)2+$\sqrt{3}$c,
∴当x=$\frac{1}{3}$时,S取得最大值,最大值为 $\sqrt{3}$c.
点评 本题考查二次函数综合题、一次函数的应用、一元二次方程的根与系数的关系等知识,解题的关键是理解新定义,学会利用方程组解决两个函数图象的交点问题,学会构建二次函数利用二次函数的性质解决最值问题,属于中考压轴题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
 如图,教室里放有一台饮水机,课间同学们依次用茶杯接水,假设接水过程中水不发生泼洒,每个同学所接的水量相等;两个放水管同时打开时,它们的流量相同.若只打开一个阀门2分钟后,再同时打开第二个阀门,(放水过程中阀门不关).饮水机的存水量(升)与放水时间(分)之间的关系如表所示:
如图,教室里放有一台饮水机,课间同学们依次用茶杯接水,假设接水过程中水不发生泼洒,每个同学所接的水量相等;两个放水管同时打开时,它们的流量相同.若只打开一个阀门2分钟后,再同时打开第二个阀门,(放水过程中阀门不关).饮水机的存水量(升)与放水时间(分)之间的关系如表所示:| 放水时间(分) | 0 | 2 | 12 | … |
| 饮水机中存水量(升) | 18 | 17 | 8 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com