
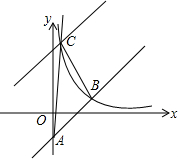
 如图,已知直线y=x+a与y轴相交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点B(-a+1,a+4).
如图,已知直线y=x+a与y轴相交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点B(-a+1,a+4).分析 (1)利用待定系数法即可解决.
(2)观察图象,直线y=x+a在反比例函数y=$\frac{k}{x}$的上方,由此可以写出不等式的解集.
(3)设平移后的直线与y轴交于点N,作AM⊥NC,垂足为M,求出AM,再证明△AMN是等腰直角三角形,求出线段AN即可解决问题.
解答 解:(1)∵点B(-a+1,a+4)在直线y=x+a上,
∴a+4=-a+1+a,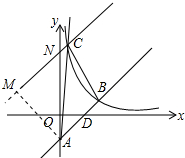
∴a=-3,点B坐标(4,1),
∵点B在y=$\frac{k}{x}$上,
∴k=4,
∴a=-3,反比例函数为y=$\frac{4}{x}$.
(2)刚才图象可知x>0时不等式x+a>$\frac{k}{x}$的解集是x>4.
(3)设平移后的直线与y轴交于点N,作AM⊥NC,垂足为M,
∵点A坐标(0,-3),点B坐标(4,1),
∴AB=4$\sqrt{2}$,
∵S△ABC=28,
∴$\frac{1}{2}$•AB•AM=28,
∴AM=7$\sqrt{2}$,
∵直线AB与x轴交点D坐标为(3,0),
∴AO=OD=3,
∴∠OAD=45°,
∵AM⊥CN,CN∥AB,
∴AB⊥AM,
∴∠MAB=90°,
∴∠MAN=45°,
∴∠MAN=∠MNA=45°,
∴MN=AM=7$\sqrt{2}$,
∴AN=14,
∴直线AB:y=x-3向上平移14个单位得到直线CN,
∴直线CN为y=x+11.
∴平移后的直线的解析式y=x+11.
点评 本题考查反比例函数与一次函数的交点、函数图象平移问题,解题的关键是记住平移规律,“上加下减,左加右减”,学会观察图象确定自变量取值范围,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
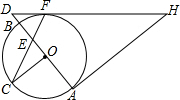 如图,在⊙O中,AB为直径,OC⊥AB,弦CF与OB交于点E,过点F,A分别作⊙O的切线交于点H,且HF与AB的延长线交于点D.
如图,在⊙O中,AB为直径,OC⊥AB,弦CF与OB交于点E,过点F,A分别作⊙O的切线交于点H,且HF与AB的延长线交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
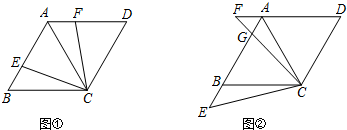
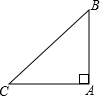 如图,在Rt△ABC中,∠BAC=90°,AB=AC.
如图,在Rt△ABC中,∠BAC=90°,AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
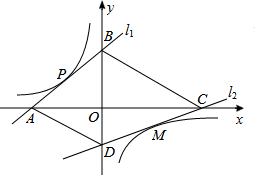 如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(-1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )
如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(-1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )| A. | (1,-1) | B. | (2,-$\frac{1}{2}$) | C. | (3,-$\frac{1}{3}$) | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
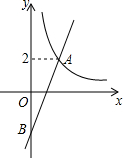 如图,在平面直角坐标系xOy中,双曲线y=$\frac{4}{x}$(x>0)与直线y=kx-k的交点为A(m,2).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{4}{x}$(x>0)与直线y=kx-k的交点为A(m,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com