
【题目】如图,矩形ABCD中,AB=9,AD=4. E为CD边上一点,CE=6. 点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
⑴求AE的长;
⑵当t为何值时,△PAE为直角三角形?
⑶是否存在这样的t,使EA恰好平分∠PED,若存在,求出t的值;若不存在,请说明理由.

【答案】(1)5;(2)6或![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)在直角△ADE中,利用勾股定理进行解答;
(2)需要分类讨论:AE为斜边和AP为斜边两种情况下的直角三角形;
(3)假设存在.利用角平分线的性质,平行线的性质以及等量代换推知:∠PEA=∠EAP,则PE=PA,由此列出关于t的方程,通过解方程求得相应的t的值即可.
试题解析:(1)∵矩形ABCD中,AB=9,AD=4,
∴CD=AB=9,∠D=90°,
∴DE=9﹣6=3,
∴AE=![]() =5;
=5;
(2)①若∠EPA=90°,t=6;
②若∠PEA=90°,![]() ,
,
解得t=![]() .
.
综上所述,当t=6或t=![]() 时,△PAE为直角三角形;
时,△PAE为直角三角形;
(3)假设存在.
∵EA平分∠PED,
∴∠PEA=∠DEA.
∵CD∥AB,
∴∠DEA=∠EAP,
∴∠PEA=∠EAP,
∴PE=PA,
∴![]() ,
,
解得t=![]() .
.
∴满足条件的t存在,此时t=![]() .
.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】经过十多年的成长,中国城市观众到影院观影的习惯已经逐渐养成:2010年,某影院观众人次总量才23400,但到2016年已经暴涨至13.5万.其中13.5万用科学计数法表示为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
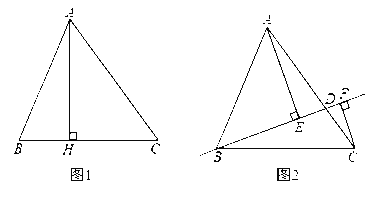
【题目】如图1和2,在△ABC中,AB=13,BC=14,BH=5.
探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积![]() ;
;
拓展:如图2,点D在AC上(可与点A,C重合),分别过点A.C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为![]() )
)
(1)用含x,m,n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,直接写出这样的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在中考体育达标跳绳项目测试中,1分钟跳160次为达标,小敏记录了他预测时1分钟跳的次数分别为145,155,140,162,164,则他在该次预测中达标的概率是___。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒。
(1)当t=3秒时,求△ABP的面积;
(2)当t为何值时,点P与点A的距离为5cm?
(3)当t为何值时(2<t<5),以线段AD、CP、AP的长度为三角形是直角三角形,且AP是斜边。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com