
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
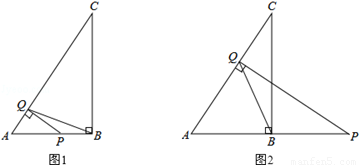
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
(1)见解析;(2)AP的长为 或6.
或6.
【解析】
试题分析:(1)由两对角相等(∠APQ=∠C,∠A=∠A),证明△APQ∽△ABC.
(2)当△PQB为等腰三角形时,有两种情况,需要分类讨论.
(I)当点P在线段AB上时,如题图1所示.由三角形相似(△APQ∽△ABC)关系计算AP的长;
(II)当点P在线段AB的延长线上时,如题图2所示.利用角之间的关系,证明点B为线段AP的中点,从而可以求出AP.
试题解析:
(1)证明:∵∠A+∠APQ=90°,∠A+∠C=90°,∴∠APQ=∠C.
在△APQ与△ABC中,∵∠APQ=∠C,∠A=∠A,
∴△APQ∽△ABC.
(2)在Rt△ABC中,AB=3,BC=4,由勾股定理得:AC=5.
∵∠BPQ为钝角,∴当△PQB为等腰三角形时,只可能是PB=PQ.
(I)当点P在线段AB上时,如题图1所示,
由(1)可知,△APQ∽△ABC,
∴ ,即
,即 ,解得:
,解得: .
.
∴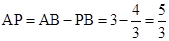 .
.
(II)当点P在线段AB的延长线上时,如题图2所示,
∵BP=BQ,∴∠BQP=∠P.
∵∠BQP+∠AQB=90°,∠A+∠P=90°,∴∠AQB=∠A.∴BQ=AB.
∴AB=BP,点B为线段AB中点.
∴AP=2AB=2×3=6.
综上所述,当△PQB为等腰三角形时,AP的长为 或6.
或6.
考点:1.相似三角形的判定与性质;2.等腰三角形的性质;3.直角三角形斜边上的中线;4.勾股定理.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
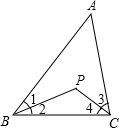 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com