
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+3(a≠0)经过(1,0),且与y轴交于点C.
(1)直接写出点C的坐标 ;
(2)求a,b的数量关系;
(3)点D(t,3)是抛物线y=ax2+bx+3上一点(点D不与点C重合).
①当t=3时,求抛物线的表达式;
②当3<CD<4时,求a的取值范围.

【答案】(1)(0,3);(2)a+b+3=0;(3)y=![]() x2﹣
x2﹣![]() x+3;②1<a<
x+3;②1<a<![]() .
.
【解析】
(1)令x=0,y的值即为C的纵坐标.
(2)把(1,0)带入即可.
(3)把D点及C点代入抛物线,得到a,b的不等式关系![]() <-
<-![]() <2,再结合(2)中的b=﹣a﹣3可得a的范围.
<2,再结合(2)中的b=﹣a﹣3可得a的范围.
解:(1)由题意得:点C的坐标(0,3);
故答案为:(0,3);
(2)把(1,0)代入抛物线y=ax2+bx+3中,
得:a+b+3=0;
(3)①把(3,3)和(1,0)代入抛物线y=ax2+bx+3中,9a+3b+3=3,a+b+3=0,求得a=![]() ,b=-
,b=-![]() .
.
∴抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x+3;
x+3;
②∵抛物线经过C(0,3)和D(t,3)两点,
∴对称轴是:x=![]() CD,CD∥x轴,
CD,CD∥x轴,
∵抛物线y=ax2+bx+3(a≠0)经过(1,0),
∴a>0,
∵3<CD<4,
∴![]() <-
<-![]() <2,
<2,
由(2)知:b=﹣a﹣3,
∴![]() <
<![]() <2
<2
∴1<a<![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是BA延长线上一点,CD切⊙O于D点,弦DE∥CB,Q是AB上一动点,CA=1,CD是⊙O半径的![]() 倍.
倍.
(1)求⊙O的半径R;
(2)当Q从A向B运动的过程中,图中阴影部分的面积是否发生变化?若发生变化,请你说明理由;若不发生变化,请你求出阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提倡“保护自然资源,节约自然资源”,某部门对某县一次性筷子的用量进行了调查.2015年从该县600家高、中、低档饭店中抽取了10家进行调查,得知这些饭店每天消耗的一次性筷子的盒数分别为:0.6,3.7,2.2,1.5,2.8,1.7,1.2,2.1,3.2,1.0.
(1)估计该县2015年各饭店共消耗多少盒一次性筷子?(一年按350个营业日计算)
(2)在(1)的条件下,若生产一套学生课桌椅需木材0.07 m3,则该县2015年各饭店使用一次性筷子所消耗的木材可以生产多少套学生课桌椅?(计算中需用到的有关数据为:每盒筷子100双,每双筷子的质量为5 g,所用木材的密度为0.5×103 kg/m3)
(3)通过以上计算,你对保护自然资源有什么看法?请提出两条合理的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2﹣2ax﹣3(a≠0)的图象经过点A.
(1)求二次函数的对称轴;
(2)当A(﹣1,0)时,
①求此时二次函数的表达式;
②把y=ax2﹣2ax﹣3化为y=a(x﹣h)2+k的形式,并写出顶点坐标;
③画出函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
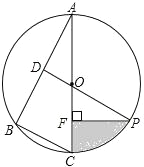
【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=4,点D是AB的中点,连接DO并延长交⊙O于点P.
(1)求劣弧PC的长(结果保留π);
(2)过点P作PF⊥AC于点F,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
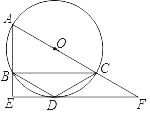
【题目】如图,已知AC是⊙O的直径,B为⊙O上一点,D为![]() 的中点,过D作EF∥BC交AB的延长线于点E,交AC的延长线于点F.
的中点,过D作EF∥BC交AB的延长线于点E,交AC的延长线于点F.
(Ⅰ)求证:EF为⊙O的切线;
(Ⅱ)若AB=2,∠BDC=2∠A,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
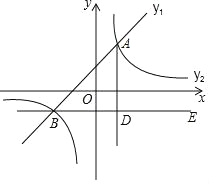
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图象与反比例函数y2=![]() 的图象交于点A(1,2)和B(﹣2,m).
的图象交于点A(1,2)和B(﹣2,m).
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1≥y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若∠DAC=30°,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
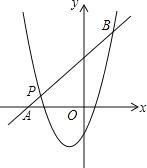
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com