
已知:关于x的方程mx2+(3m+1)x+3=0.
(1)求证:不论m为任何实数,此方程总有实数根;
(2)如果该方程有两个不同的整数根,且m为正整数,求m的值;
(3)在(2)的条件下,令y=mx2+(3m+1)x+3,如果当x1=a与x2=a+n(n≠0)时有y1=y2,求代数式4a2+12an+5n2+16n+8的值.
解:(1)当m=0时,原方程化为x+3=0,此时方程有实数根 x=-3.…………1分
当m≠0时,原方程为一元二次方程.
∵△=(3m+1)2-12m=9m2-6m+1=(3m-1)2.
∵m≠0,∴不论m为任何实数时总有(3m-1)2≥0.
∴此时方程有两个实数根.………………………………………………2分
综上,不论m为任何实数时,方程 mx2+(3m+1)x+3=0总有实数根.
(2)∵mx2+(3m+1)x+3=0.
解得 x1=-3,x2=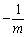 . ………………………………………………3分
. ………………………………………………3分
∵方程mx2+(3m+1)x+3=0有两个不同的整数根,且m为正整数,
∴m=1.………………………………………………………………………5分
(3)∵m=1,y=mx2+(3m+1)x+3.
∴y=x2+4x+3.
又∵当x1=a与x2=a+n(n≠0)时有y1=y2,
∴当x1=a时,y1=a2+4a+3,
当x2=a+n时,y2=(a+n)2+4(a+n)+3.
∴a2+4a+3=(a+n)2+4(a+n)+3.
化简得 2an+n2+4n=0.
即 n(2a+n+4)=0.
又∵n≠0,∴2a=-n-4.
∴ 4a2+12an+5n2+16n+8
=(2a)2+2a•6n+5n2+16n+8
=(n+4)2+6n(-n-4)+5n2+16n+8=24.


科目:初中数学 来源: 题型:
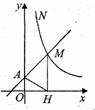 如图,直线y=x+1与y轴交于A点,与反比列函数y=
如图,直线y=x+1与y轴交于A点,与反比列函数y= (x>
(x>
0)的图象交于点M,过M作MH⊥x,且tan∠AHO=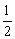 .
.
(1)求k的值;
(2)设点N(1,a)是反比例函数y= (x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BEC≌△DFC;
(2)如果BC+DF=9,CF=3,求正方形ABCD的面积.
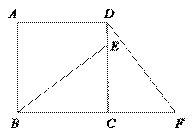
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两个盒子中装有质地、大小相同的小球,甲盒中有2个白球,1个黄球和1个蓝球;乙盒中有1个白球,2个黄球和若干个蓝球.从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍.
⑴ 求乙盒中蓝球的个 数;
数;
⑵ 从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com