
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款2.4万元,乙工程队工程款1万元.工程领导小组根据甲,乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用12天;
(3)若甲,乙两队合做6天,余下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
【答案】在不耽误工期的前提下,选第三种施工方案最节省工程款.
【解析】
关键描述语为:“甲,乙两队合做3天,余下的工程由乙队单独做也正好如期完成”;说明甲队实际工作了3天,乙队工作了x天完成任务,工作量=工作时间×工作效率等量关系为:甲3天的工作量+乙规定日期的工作量=1列方程.再看费用情况:方案(1)、(3)不耽误工期,符合要求,可以求费用,方案(2)显然不符合要求.
解:设规定日期为x天.由题意得
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
经检验:x=12是原方程的根.
方案(1):2.4×12=28.8(万元);
方案(2)比规定日期多用12天,显然不符合要求;
方案(3):2.4×6+1×12=26.4(万元).
∵28.8>26.4,
∴在不耽误工期的前提下,选第三种施工方案最节省工程款.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在进行二次根式的化简与运算时,我们有时会碰上如![]() 样的式子,其实我们还可以将其进一步化简:
样的式子,其实我们还可以将其进一步化简:
(1)![]() ···(一)
···(一)
(2)![]() ···(二)
···(二)
(3) ···(三)
···(三)
以上这种化简的步骤叫做分母有理化.
![]() 还可以用以下方法化简:
还可以用以下方法化简: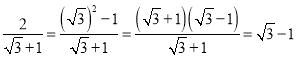 ···(四)
···(四)
请完成下列问题:
(1)请计算![]() ;
;
(2)当![]() ,则代数式
,则代数式![]() 的值为 ;
的值为 ;
(3)请参照(三)式和(四)式用两种不同的方法化简![]()
(4)化简:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种旅游纪念品,第一周的营业额为200元,第二周该商店对纪念品打8折销售,结果销售量增加3件,营业额增加了40%.
(1)求该商店第二周的营业额;
(2)求第一周该种纪念品每件的销售价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB的中点,点D在线段CB上.
![]()
(1)图中共有 条线段.
(2)图中AD=AC+CD,BC=AB﹣AC,类似地,请你再写出两个有关线段的和与差的关系式:
① ;② .
(3)若AB=8,DB=1.5,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内,如图,在平行四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 边上任意一点,连接
边上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 的大小.
的大小.
(![]() )当
)当![]() 时,求点
时,求点![]() 与点
与点![]() 间的距离(结果保留根号).
间的距离(结果保留根号).
(![]() )若点
)若点![]() 恰好落在平行四边形
恰好落在平行四边形![]() 的边所在的条直线上,直接写出
的边所在的条直线上,直接写出![]() 旋转到
旋转到![]() 所扫过的面积(结果保留
所扫过的面积(结果保留![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点B、C为线段AD上的两点,AB=![]() BC=
BC=![]() CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
查看答案和解析>>
科目:初中数学 来源: 题型:
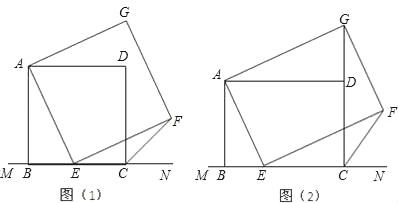
【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com